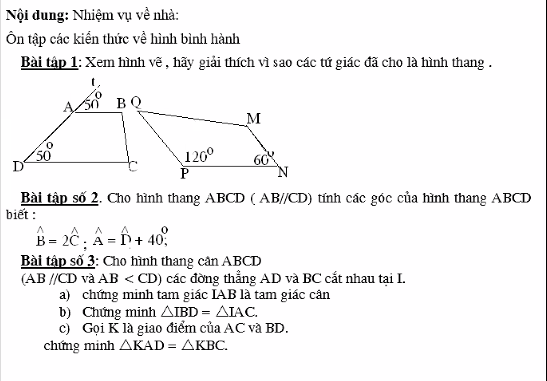
a) Ta có: \(x^2-3=0\)
nên \(x^2=3\)
hay \(x\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
b) Ta có: \(4x^2-9=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
c) Ta có: \(\left(x+2\right)^2-\left(x-2\right)^2=5\)
\(\Leftrightarrow x^2+4x+4-x^2+4x-4=5\)
\(\Leftrightarrow8x=5\)
hay \(x=\dfrac{5}{8}\)
d) Ta có: \(\left(x+2\right)^3-x^3+6x^2=7\)
\(\Leftrightarrow x^3+6x^2+12x+8-x^3+6x^2-7=0\)
\(\Leftrightarrow12x^2+12x+1=0\)
\(\Delta=12^2-4\cdot12\cdot1=144-48=96\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-4\sqrt{6}}{24}=\dfrac{-3-\sqrt{6}}{6}\\x_2=\dfrac{-12+4\sqrt{6}}{24}=\dfrac{-3+\sqrt{6}}{6}\end{matrix}\right.\)
e) Ta có: \(\left(x-2\right)^2-\left(x-1\right)\left(x+1\right)=7\)
\(\Leftrightarrow x^2-4x+4-x^2+1=7\)
\(\Leftrightarrow-4x=2\)
hay \(x=-\dfrac{1}{2}\)



 help mik vs mai phải nộp r;-;
help mik vs mai phải nộp r;-;