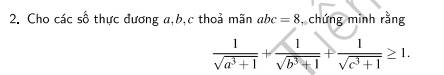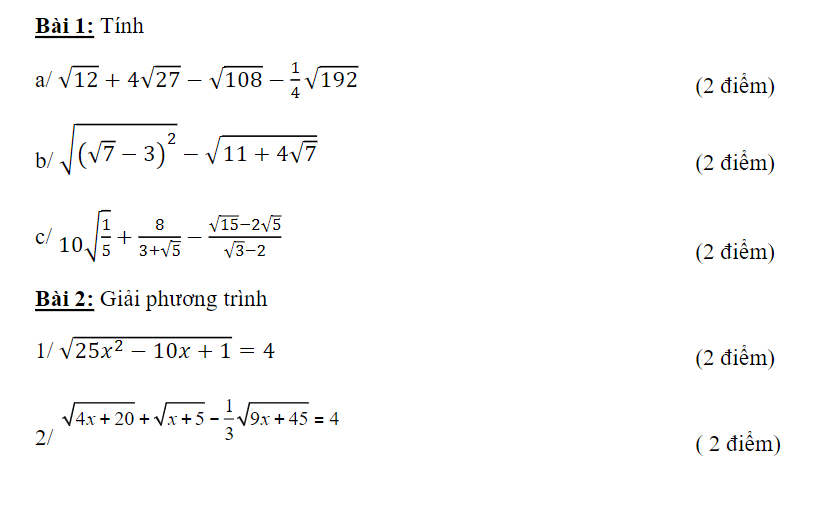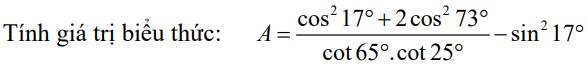\(đka\ne b,a>0;b>0\)
\(=\left(\dfrac{2\sqrt{ab}}{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{\sqrt{a}+\sqrt{b}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\right):\dfrac{1}{\sqrt{a}-\sqrt{b}}\\ =\left(\dfrac{2}{\sqrt{a}-\sqrt{b}}-\dfrac{1}{\sqrt{a}-\sqrt{b}}\right):\dfrac{1}{\sqrt{a}-\sqrt{b}}\\ =\dfrac{1}{\sqrt{a}-\sqrt{b}}\times\dfrac{\sqrt{a}-\sqrt{b}}{1}\\ =1\)
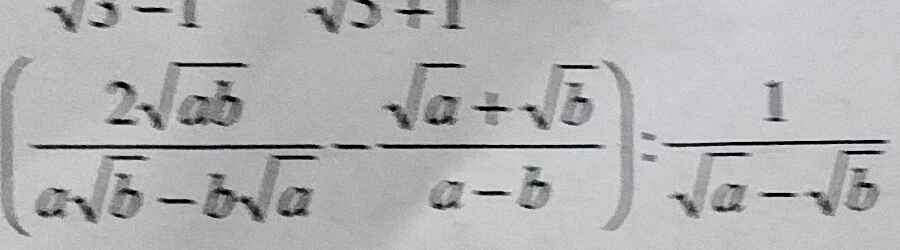


 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 


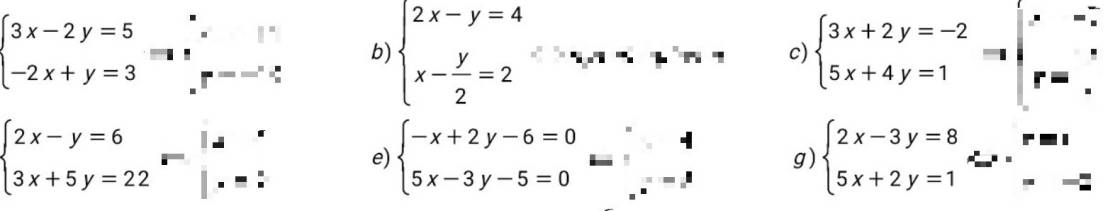
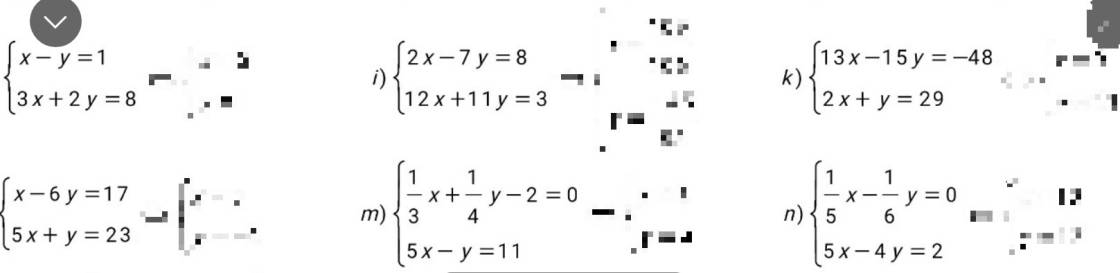 giúp mik với mik đg cần gấp
giúp mik với mik đg cần gấp