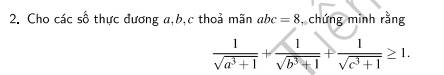Đặt \(a=\dfrac{x}{2};b=\dfrac{y}{2};c=\dfrac{z}{2}\). Khi đó \(xyz=1\).
Bất đẳng thức cần chứng minh trở thành:
\(\sum\dfrac{1}{\sqrt{8x^3+1}}\ge1\)
Ta có: \(\sum\dfrac{1}{\sqrt{8x^3+1}}=\sum\sqrt{\dfrac{b^3c^3}{8+b^3c^3}}=\sum\dfrac{b^2c^2}{\sqrt{8bc+b^4c^4}}\ge\dfrac{\left(ab+bc+ca\right)^2}{\sum\sqrt{8bc+b^4c^4}}=\dfrac{\sum b^2c^2+2\sum a}{\sum\sqrt{8bc+b^4c^4}}\ge\dfrac{\sum b^2c^2+6}{\sum\sqrt{8bc+b^4c^4}}\)
Phép chứng minh sẽ hoàn tất nếu ta chứng minh được:
\(\sum b^2c^2+6\ge\sum\sqrt{8bc+b^4c^4}\left(\cdot\right)\)
Để ý rằng, nếu ta chứng minh được \(b^2c^2+2\ge\sqrt{8bc+b^4c^4}\left(1\right)\) thì ta sẽ chứng minh được (*).
Thật vậy, bằng phép biến đổi tương đương, ta có:
\(b^2c^2+2\ge\sqrt{8bc+b^4c^4}\)
\(\Leftrightarrow b^4c^4+4b^2c^2+4\ge8bc+b^4c^4\)
\(\Leftrightarrow4\left(bc-1\right)^2\ge0\) (luôn đúng).
Vậy nhận xét (1) là đúng. Từ đây ta có điều phải chứng minh.
Dấu "=" xảy ra khi \(a=b=c=2\)
Đặt \(A=\dfrac{1}{\sqrt{a^3+1}}+\dfrac{1}{\sqrt{b^3+1}}+\dfrac{1}{\sqrt{c^3+1}}\)
\(\sqrt{a^3+1}=\sqrt{\left(a+1\right)\left(a^2-a+1\right)}\)
=>\(\sqrt{a^3+1}< =\dfrac{a+1+a^2-a+1}{2}=\dfrac{a^2+2}{2}\)
=>\(\dfrac{1}{\sqrt{a^3+1}}>=\dfrac{2}{a^2+2}\)
Chứng minh tương tự, ta được:
\(\sqrt{b^3+1}< =\dfrac{b^2+2}{2}\) và \(\sqrt{c^3+1}< =\dfrac{c^2+2}{2}\)
=>\(\dfrac{1}{\sqrt{b^3+1}}>=\dfrac{2}{b^2+2};\dfrac{1}{\sqrt{c^3+1}}>=\dfrac{2}{c^2+2}\)
=>\(\dfrac{1}{\sqrt{a^3+1}}+\dfrac{1}{\sqrt{b^3+1}}+\dfrac{1}{\sqrt{c^3+1}}>=\dfrac{2}{a^2+2}+\dfrac{2}{b^2+2}+\dfrac{2}{c^2+2}\)
=>\(A>=\dfrac{2}{a^2+2}+\dfrac{2}{b^2+2}+\dfrac{2}{c^2+2}\)
=>\(A>=\dfrac{2\left(b^2+2\right)\left(c^2+2\right)+2\left(a^2+2\right)\left(c^2+2\right)+2\left(b^2+2\right)\left(a^2+2\right)}{\left(a^2+2\right)\left(c^2+2\right)\left(b^2+2\right)}\)
=>\(A>=\dfrac{2\left(b^2c^2+2c^2+2b^2+4+a^2c^2+2a^2+2c^2+4+a^2b^2+2b^2+2a^2+4\right)}{\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)}\)
=>\(A>=\dfrac{2\left(a^2b^2+b^2c^2+c^2a^2\right)+8\left(a^2+b^2+c^2\right)+24}{\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)}\)
=>\(A>=\dfrac{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+24+4\left(a^2+b^2+c^2\right)}{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+8+8^2}\)(Vì abc=8)
Ta lại có: \(a^2+b^2+c^2>=3\sqrt[3]{a^2b^2c^2}=3\cdot\sqrt[3]{8^2}=12\)
=>\(4\left(a^2+b^2+c^2\right)>=48\)
=>\(A>=\dfrac{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+24+48}{2\left(a^2b^2+b^2c^2+a^2c^2\right)+4\left(a^2+b^2+c^2\right)+8+64}\)
=>A>=1(ĐPCM)