a.
Theo tính chất lập phương, \(CC'\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của \(AC'\) lên (ABCD)
\(\Rightarrow\widehat{C'AC}\) là góc giữa AC' và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=4\sqrt{2}\)
\(\Rightarrow tan\widehat{C'AC}=\dfrac{CC'}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{C'AC}\approx35^016'\)
b.
Theo t/c lập phương, \(CD\perp\left(BCB'\right)\)
Mà CD là giao tuyến (A'B'CD) và (ABCD)
\(\Rightarrow\widehat{BCB'}\) là góc giữa (A'B'CD) và (ABCD)
\(tan\widehat{BCB'}=\dfrac{BB'}{BC}=\dfrac{4}{4}=1\Rightarrow\widehat{BCB'}=45^0\)
c.
\(AA'\perp\left(A'B'C'D'\right)\Rightarrow AA'\perp A'P\Rightarrow\Delta MA'P\) vuông tại A'
\(\Rightarrow MP=\sqrt{A'M^2+A'P^2}=\sqrt{A'M^2+A'D'^2+D'P^2}\)
\(=\sqrt{2^2+4^2+2^2}=2\sqrt{6}\left(cm\right)\)
Tương tự:
\(MN=\sqrt{AM^2+AB^2+BN^2}=2\sqrt{6}\left(cm\right)\)
\(NP=\sqrt{C'P^2+C'C^2+CN^2}=2\sqrt{6}\left(cm\right)\)
\(\Rightarrow MN=MP=NP\Rightarrow\Delta MNP\) đều
\(\Rightarrow S_{\Delta MNP}=\dfrac{MN^2\sqrt{3}}{4}=6\sqrt{3}\left(cm^2\right)\)
d.
Gọi Q là trung điểm CD \(\Rightarrow PQ\perp\left(ABCD\right)\)
\(\Rightarrow\Delta ANQ\) là hình chiếu vuông góc của tam giác MNP lên (ABCD)
\(S_{\Delta ANQ}=S_{ABCD}-S_{ADQ}-S_{ABN}-S_{CNQ}\)
\(=AB^2-\dfrac{1}{2}AD.DQ-\dfrac{1}{2}AB.BN-\dfrac{1}{2}CQ.CN\)
\(=4^2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.2.2=6\left(cm^2\right)\)
\(\Rightarrow cos\alpha=\dfrac{S_{AQN}}{S_{MNP}}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\Rightarrow\alpha\approx54^044'\)
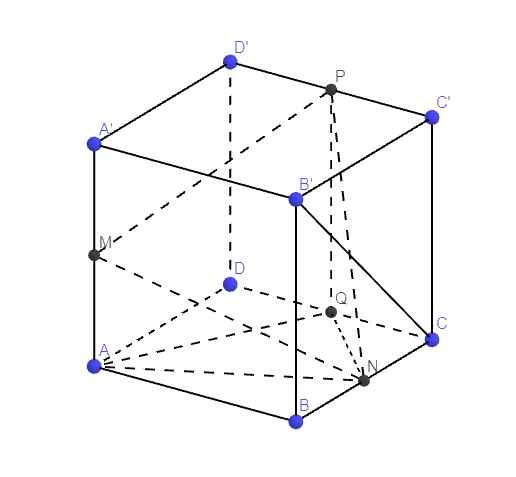
câu 3 5c mn giúp em cần gấp lắm ạ
