1: Thay x=9 vào A, ta được:
\(A=\dfrac{2\cdot3+6}{9-1}=\dfrac{6+6}{8}=\dfrac{12}{8}=1,5\)
2: \(B=\dfrac{x+2}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+2-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{1}{\sqrt{x}-1}\)
3: \(\dfrac{A}{B}=\dfrac{2\sqrt{x}+6}{x-1}:\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\left(\sqrt{x}-1\right)=\dfrac{2\sqrt{x}+6}{\sqrt{x}+1}\)
\(\dfrac{A}{B}-6=\dfrac{2\sqrt{x}+6}{\sqrt{x}+1}-6=\dfrac{2\sqrt{x}+6-6\sqrt{x}-6}{\sqrt{x}+1}=\dfrac{-4\sqrt{x}}{\sqrt{x}+1}< =0\)
=>\(\dfrac{A}{B}< =6\)
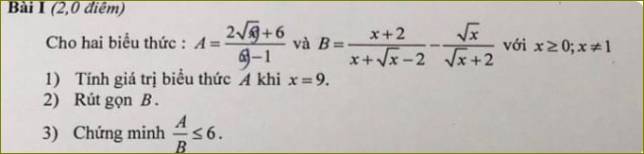
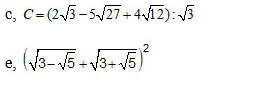
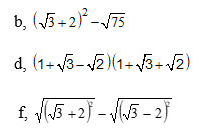các bạn giải hộ mik mấy câu này vs mik đag cần gấp
