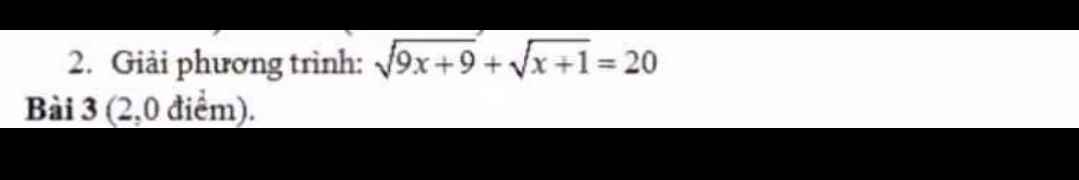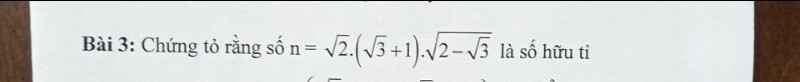\(B=\dfrac{\sqrt{x-2}}{x}+\dfrac{\sqrt{y-1}}{y}=\dfrac{\sqrt{2\left(x-2\right)}}{x\sqrt{2}}+\dfrac{\sqrt{1.\left(y-1\right)}}{y}\le^{Caushy}\dfrac{\dfrac{x-2+2}{2}}{x\sqrt{2}}+\dfrac{\dfrac{y-1+1}{2}}{y}=\dfrac{x}{x.2\sqrt{2}}+\dfrac{y}{2y}=\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2}=\dfrac{2+\sqrt{2}}{4}\)Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-2=2\\y-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\left(n\right)\\y=2\left(n\right)\end{matrix}\right.\)
Vậy \(MaxB=\dfrac{2+\sqrt{2}}{4}\)