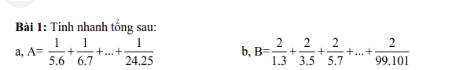A = 1/(5.6) + 1/(6.7) + ... + 1/(24.25)
= 1/5 - 1/6 + 1/6 - 1/7 + ... + 1/24 - 1/25
= 1/5 - 1/25
= 4/25
B = 2/(1.3) + 2/(3.5) + 2/(5.7) + ... + 2/(99.101)
= 1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ... + 1/99 - 1/101
= 1 - 1/101
= 100/101
`a) A = 1/(5.6) + 1/(6.7)+...+1/(24.25)`
`= 1/5 - 1/6 + 1/6 - 1/7 +...+1/24-1/25`
`= 1/5-1/25`
`= 5/25 - 1/25`
`= 4/25`
Vậy:`A = 4/25`
`b) B = 2/(1.3)+2/(3.5)+...+2/(99.101)`
`= 1- 1/3 + 1/3 - .... +1/99-1/101`
`= 1 - 1/101`
`= 100/101`
Vậy: `B = 100/101`