111.
ĐKXĐ: \(x>\dfrac{1}{2}\)
\(log_2x.log_3\left(2x-1\right)< 2log_2x\)
\(\Leftrightarrow log_2x\left[log_3\left(2x-1\right)-2\right]< 0\)
TH1: \(\left\{{}\begin{matrix}log_2x< 0\\log_3\left(2x-1\right)>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}< x< 1\\2x-1>9\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại x thỏa mãn
TH2: \(\left\{{}\begin{matrix}log_2x>0\\log_3\left(2x-1\right)< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>1\\2x-1< 9\end{matrix}\right.\)
\(\Rightarrow1< x< 5\)
\(\Rightarrow x=\left\{2;3;4\right\}\) có 3 giá trị nguyên
112.
ĐKXĐ: \(x>0\)
\(\Leftrightarrow log_2^2\left(\dfrac{8}{x^2}\right)-log_2x-log_24< -2\)
\(\Leftrightarrow\left(log_28-log_2x^2\right)^2-log_2x< 0\)
\(\Leftrightarrow\left(3-2log_2x\right)^2-log_2x< 0\)
\(\Leftrightarrow4log_2^2x-13log_2x+9< 0\)
\(\Leftrightarrow1< log_2x< \dfrac{9}{4}\)
\(\Rightarrow1< x< 2^{\dfrac{9}{4}}\Rightarrow x=\left\{2;3;4\right\}\)
Có 3 giá trị nguyên
113.
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\3-log_5x\ge0\end{matrix}\right.\) \(\Rightarrow0< x\le125\)
\(\left(-log_2^2x+5log_2x+6\right)\sqrt{3-log_5x}\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}3-log_5x=0\\-log_2^2x+5log_2x+6\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=125\\-1\le log_2x\le6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=125\\\dfrac{1}{2}\le x\le64\end{matrix}\right.\)
\(\Rightarrow\) Có \(1+\left(64-1+1\right)=65\) số nguyên x thỏa mãn
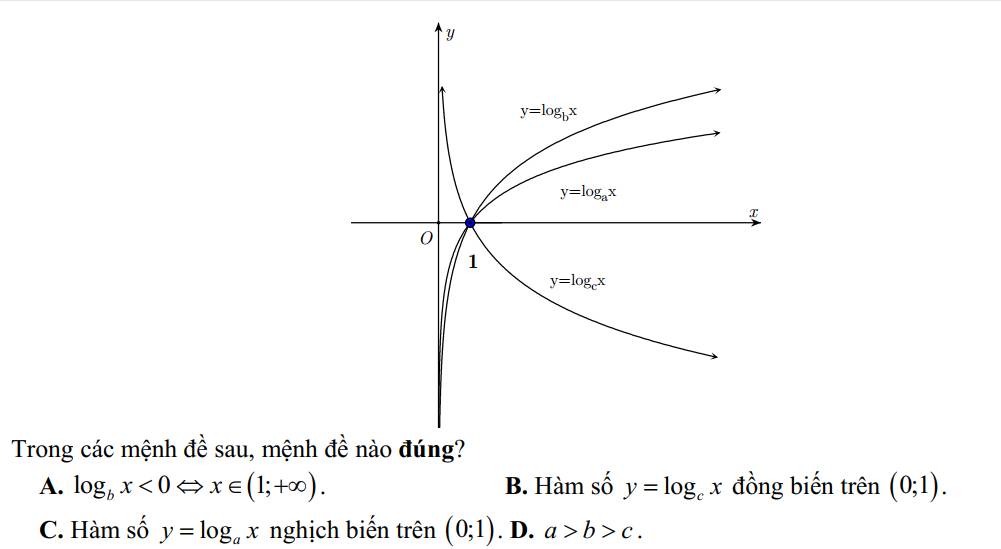
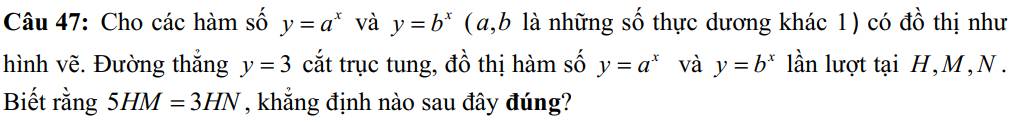
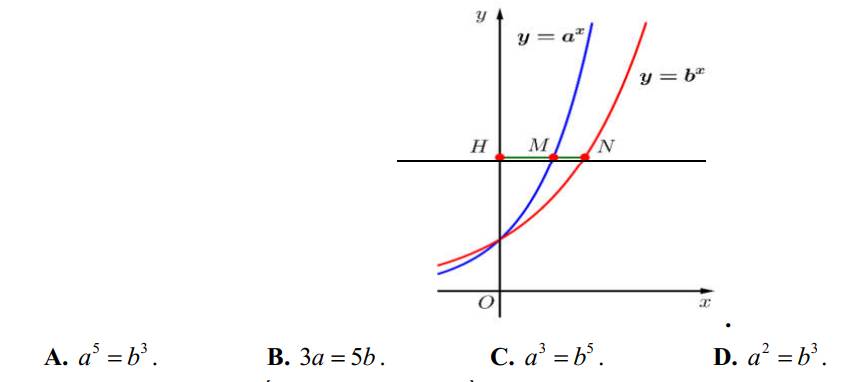
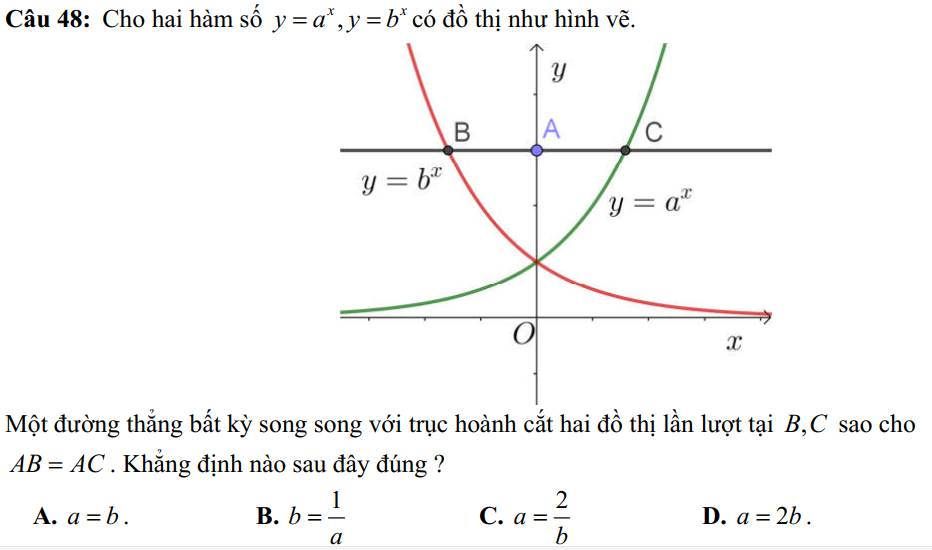
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
