`(1/3)^(x + 3) + (1/3)^(x + 2) = 4/27`
`=> (1/3)^(x + 2 + 1) + (1/3)^(x + 2) = 4/27`
`=> (1/3)^(x + 2) . 1/3 + (1/3)^(x + 2) = 4/27`
`=> (1/3)^(x + 2) . (1/3 + 1) = 4/27`
`=> (1/3)^(x + 2) . 4/3 = 4/27`
`=> (1/3)^(x + 2) = 4/27 : 4/3 = 1/9 = (1/3)^2`
`=> x +2 =2`
`=> x = 0`
Vậy `x = 0`
\(\left(\dfrac{1}{3}\right)^{x+3}+\left(\dfrac{1}{3}\right)^{x+2}=\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x.\left(\dfrac{1}{3}\right)^3+\left(\dfrac{1}{3}\right)^x.\left(\dfrac{1}{3}\right)^2=\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x.\dfrac{1}{27}+\left(\dfrac{1}{3}\right)^x.\dfrac{1}{9}=\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x\left(\dfrac{1}{27}+\dfrac{1}{9}\right)=\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x\left(\dfrac{1}{27}+\dfrac{3}{27}\right)=\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x.\dfrac{4}{27}=\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x=\dfrac{4}{27}:\dfrac{4}{27}\)
\(\left(\dfrac{1}{3}\right)^x=\dfrac{4}{27}.\dfrac{27}{4}\)
\(\left(\dfrac{1}{3}\right)^x=1\)
\(\left(\dfrac{1}{3}\right)^x=\left(\dfrac{1}{3}\right)^0\)
\(x=0\)
Vậy `x=0`

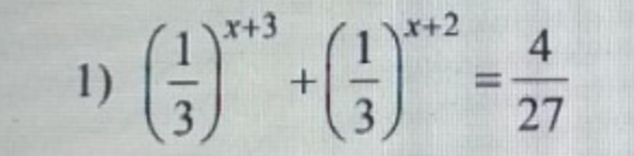



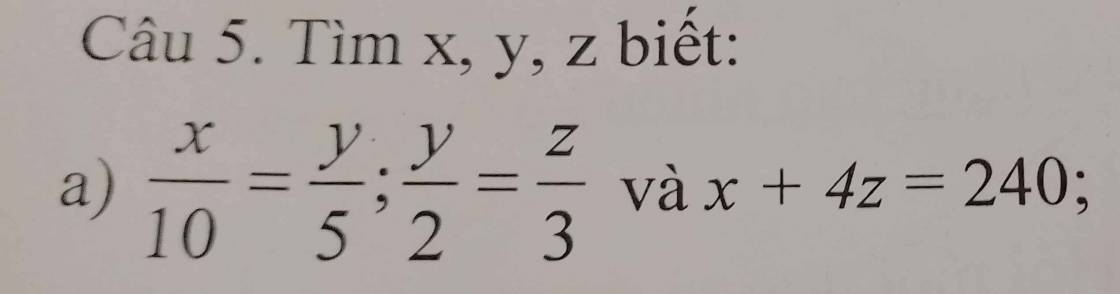
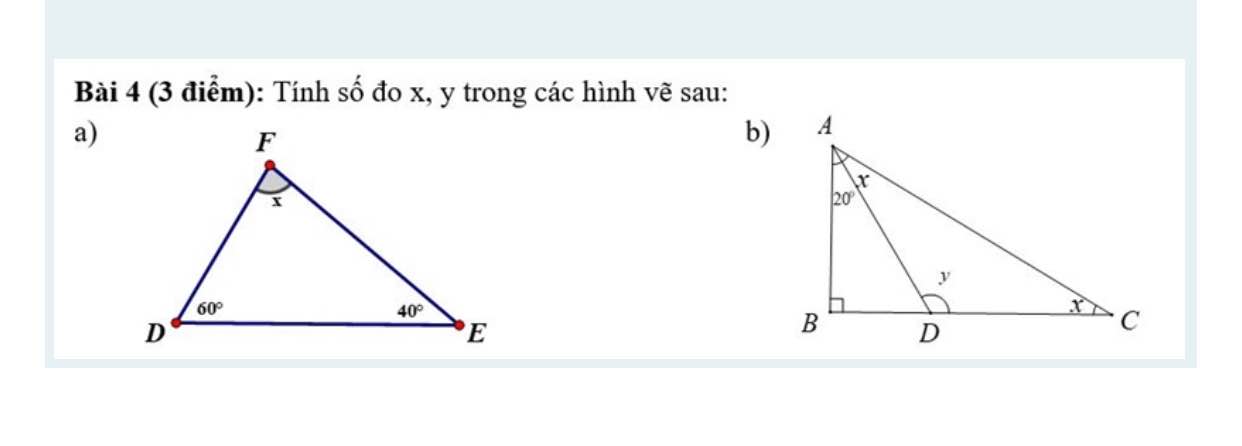
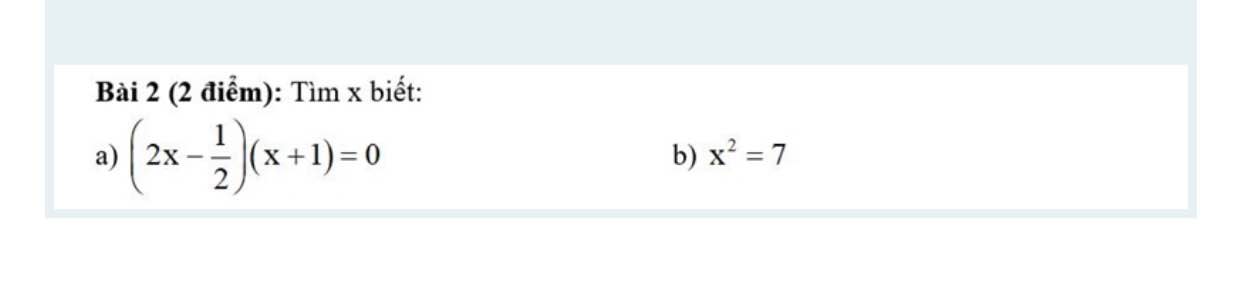


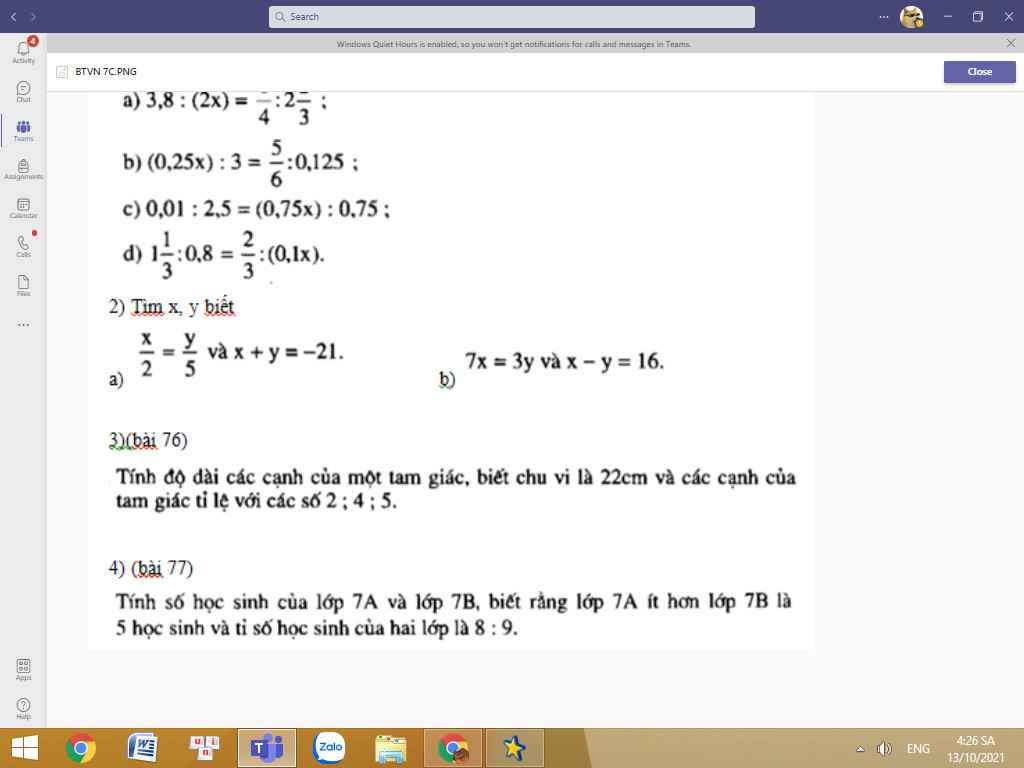 ai giúp em làm câu này vs em đang cần gấp ạ
ai giúp em làm câu này vs em đang cần gấp ạ giúp em câu này nữa ạ, làm phiền mấy anh chị rồi ạ, xl :)
giúp em câu này nữa ạ, làm phiền mấy anh chị rồi ạ, xl :)
