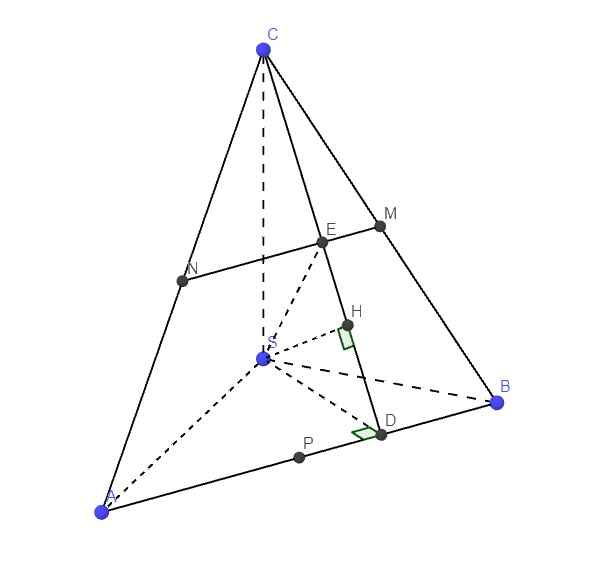
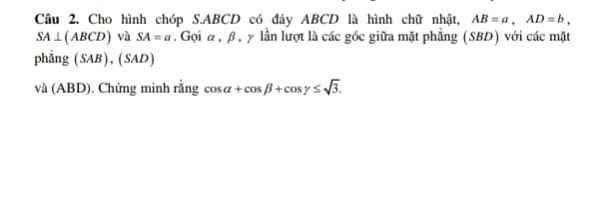Kẻ \(SD\perp AB\), kẻ \(SH\perp CD\), gọi E là giao điểm CD và MN
\(\Rightarrow SH\perp\left(ABC\right)\)
\(\Rightarrow\widehat{SEH}\) là góc giữa (SMN) và (ABC) hay \(\widehat{SEH}=\alpha\)
Đặt \(\left(SA;SB;SC\right)=\left(\dfrac{1}{\sqrt{a}};\dfrac{1}{\sqrt{b}};\dfrac{1}{\sqrt{c}}\right)\) (việc đặt này chỉ để dễ dàng cho tính toán về sau)
Hệ thức lượng: \(\dfrac{1}{SH^2}=\dfrac{1}{SD^2}+\dfrac{1}{SC^2}=\dfrac{1}{SA^2}+\dfrac{1}{SB^2}+\dfrac{1}{SC^2}=a+b+c\)
\(\Rightarrow SH=\dfrac{1}{\sqrt{a+b+c}}\)
Do MN là đường trung bình tam giác ABC \(\Rightarrow E\) là trung điểm CD hay SE là trung tuyến trong tam giác vuông SCD
\(\Rightarrow SE=\dfrac{1}{2}CD=\dfrac{1}{2}\sqrt{SC^2+SD^2}=\dfrac{1}{2}\sqrt{SC^2+\dfrac{SA^2.SB^2}{SA^2+SB^2}}\)
\(=\dfrac{1}{2}\sqrt{\dfrac{1}{c}+\dfrac{1}{a+b}}=\dfrac{1}{2}\sqrt{\dfrac{a+b+c}{c\left(a+b\right)}}\)
\(\Rightarrow sin\alpha=\dfrac{SH}{SE}=\dfrac{2\sqrt{c\left(a+b\right)}}{a+b+c}\)
Tương tự: \(sin\beta=\dfrac{2\sqrt{b\left(a+c\right)}}{a+b+c}\) ; \(sin\gamma=\dfrac{2\sqrt{a\left(b+c\right)}}{a+b+c}\)
\(\Rightarrow T=\dfrac{2\left(\sqrt{ab+ac}+\sqrt{ac+bc}+\sqrt{ab+bc}\right)}{a+b+c}\le\dfrac{2\sqrt{6\left(ab+bc+ca\right)}}{a+b+c}\)
\(T\le\dfrac{2\sqrt{2\left(a+b+c\right)^2}}{a+b+c}=2\sqrt{2}\)
Dấu "=" xảy ra khi \(a=b=c\) hay \(SA=SB=SC\)