a.
Do I là tâm hbh ABB'A' \(\Rightarrow I\) là trung điểm A'B
Lại có M là trung điểm BC theo giả thiết
\(\Rightarrow\) IM là đường trung bình tam giác A'BC
\(\Rightarrow IM||A'C\)
\(\Rightarrow IM||\left(ACC'A'\right)\)
Do \(IM\in\left(AB'M\right)\) và A là 1 điểm chung của (AB'M) và (ACC'A'), qua A kẻ đường thẳng d song song IM (và A'C) thì d là giao tuyến (AB'M) và (ACC'A')
b.
N là trung điểm A'A, I là trung điểm AB'
\(\Rightarrow IN\) là đường trung bình tam giác AA'B'
\(\Rightarrow IN||A'B'\Rightarrow IN||\left(A'B'M\right)\) (1)
Tương tự ta có IE là đtb tam giác AB'M \(\Rightarrow IE||B'M\Rightarrow IE||\left(A'B'M\right)\) (2)
(1);(2) \(\Rightarrow\left(EIN\right)||\left(A'B'M\right)\)
c.
c.
K là trung điểm B'C \(\Rightarrow IK\) là đtb tam giác AB'C
\(\Rightarrow IK||AC\)
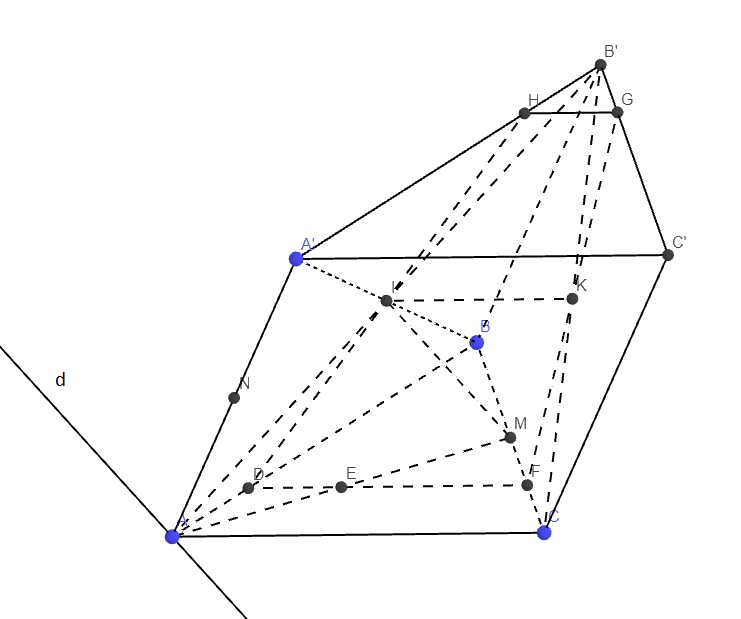
Trong mp (ABC), qua E kẻ đường thẳng song song AC cắt AB và BC lần lượt tại D và F
\(\Rightarrow DF\in\left(EIK\right)\)
Trong mp (BCC'B'), nối FK kéo dài cắt B'C' tại G
\(\Rightarrow G\in\left(EIK\right)\)
Trong mp (A'B'C'), qua G kẻ đường thẳng song song A'C' cắt A'B' tại H
\(\left\{{}\begin{matrix}GH||A'C'\\A'C'||AC||DF\end{matrix}\right.\) \(\Rightarrow GH||DF||IK\Rightarrow H\in\left(EIK\right)\)
\(\Rightarrow\) Tứ giác DFGH là thiết diện của (EIK) và lăng trụ
Theo cmt ta có \(GH||DF\Rightarrow\) thiết diện là hình thang







 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
