Lời giải:
\(P=\left[\frac{x}{\sqrt{x}(\sqrt{x}-1)}-\frac{1}{\sqrt{x}(\sqrt{x}-1)}\right]:\left[\frac{\sqrt{x}-1}{(\sqrt{x}+1)(\sqrt{x}-1)}+\frac{2}{(\sqrt{x}-1)(\sqrt{x}+1)}\right]\)
\(=\frac{x-1}{\sqrt{x}(\sqrt{x}-1)}: \frac{\sqrt{x}+1}{(\sqrt{x}+1)(\sqrt{x}-1)}\)
\(=\frac{\sqrt{x}+1}{\sqrt{x}}: \frac{1}{\sqrt{x}-1}=\frac{(\sqrt{x}+1)(\sqrt{x}-1)}{\sqrt{x}}=\frac{x-1}{\sqrt{x}}\)
b. $P< 2\Leftrightarrow \frac{x-1}{\sqrt{x}}-2<0$
$\Leftrightarrow \frac{x-1-2\sqrt{x}}{\sqrt{x}}<0$
$\Leftrightarrow x-2\sqrt{x}-1<0$
$\Leftrightarrow 1+\sqrt{2}> \sqrt{x}> 1-\sqrt{2}$
$\Leftrightarrow 1+\sqrt{2}> \sqrt{x}$
$\Leftrightarrow 3+2\sqrt{2}> x$
Vậy $x>0; x\neq 1$ và $x< 3+2\sqrt{2}$
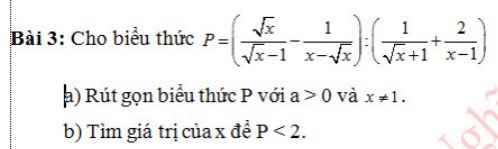










 giúp e vs ạ :<
giúp e vs ạ :<