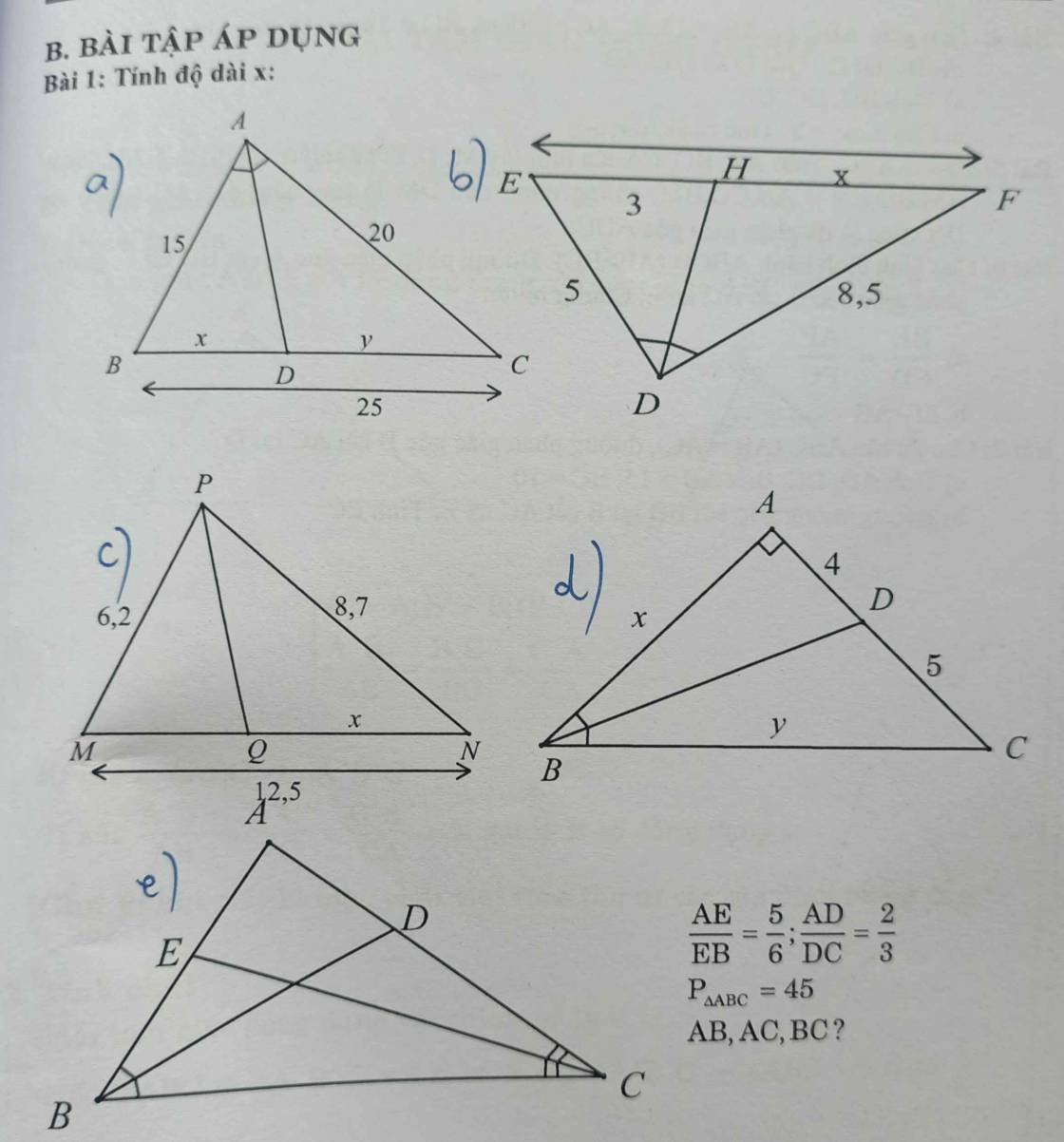
c: Xét ΔPMN có PQ là đường phân giác
nên \(\dfrac{MQ}{MP}=\dfrac{NQ}{PN}\)
=>\(\dfrac{MQ}{6,2}=\dfrac{QN}{8,7}\)
mà MQ+QN=MN=12,5
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MQ}{6,2}=\dfrac{QN}{8,7}=\dfrac{MQ+QN}{6,2+8,7}=\dfrac{12.5}{14.9}=\dfrac{125}{149}\)
=>\(\dfrac{x}{8,7}=\dfrac{125}{149}\)
=>\(x=\dfrac{125}{149}\cdot\dfrac{87}{10}=\dfrac{87\cdot25}{2\cdot149}=\dfrac{2175}{298}\)
d: Xét ΔBAC có BD là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AD}{DC}=\dfrac{4}{5}\)
=>\(\dfrac{BA}{4}=\dfrac{BC}{5}=k\)
=>BA=4k; BC=5k
=>x=4k; y=5k
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2-AB^2=AC^2\)
=>\(\left(5k\right)^2-\left(4k\right)^2=9^2\)
=>\(9k^2=81\)
=>\(k^2=9\)
=>k=3
=>\(x=4\cdot3=12;y=5\cdot3=15\)
e: Xét ΔBAC có BD là phân giác
nên \(\dfrac{BA}{BC}=\dfrac{AD}{DC}=\dfrac{2}{3}\)
=>\(\dfrac{BA}{2}=\dfrac{BC}{3}\)
=>\(\dfrac{BA}{4}=\dfrac{BC}{6}\)
Xét ΔCAB có CE là phân giác
nên \(\dfrac{CA}{CB}=\dfrac{AE}{EB}=\dfrac{5}{6}\)
=>\(\dfrac{CA}{5}=\dfrac{CB}{6}\)
=>\(\dfrac{BA}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}\)
mà \(BA+AC+BC=P_{ABC}\cdot2=90\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BA}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}=\dfrac{AB+AC+BC}{4+5+6}=\dfrac{90}{15}=6\)
=>\(AB=4\cdot6=24\left(cm\right);AC=5\cdot6=30\left(cm\right);BC=6\cdot6=36\left(cm\right)\)