\(M=\left(\dfrac{1}{a-\sqrt{a}}+\dfrac{1}{\sqrt{a}-1}\right):\dfrac{\sqrt{a}+1}{a-2\sqrt{a}+1}\\= \left(\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\dfrac{1}{\sqrt{a}-1}\right)\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\\ =\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\\ =\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b) thay a = 16 vào M ta được
\(\dfrac{\sqrt{16}-1}{\sqrt{16}}=\dfrac{3}{4}\)
c) \(\dfrac{\sqrt{a}-1}{\sqrt{a}}=\dfrac{\sqrt{a}}{\sqrt{a}}-\dfrac{1}{\sqrt{a}}=1-\dfrac{1}{\sqrt{a}}\)
để M nhận giá trị nguyên thì \(\sqrt{a}\inƯ\left(1\right)=\pm1\)
\(\sqrt{a}=1\Rightarrow a=1\left(\text{không thoả mãn}\right)\\ \sqrt{a}=-1\left(\text{không thoả mãn}\right)\)
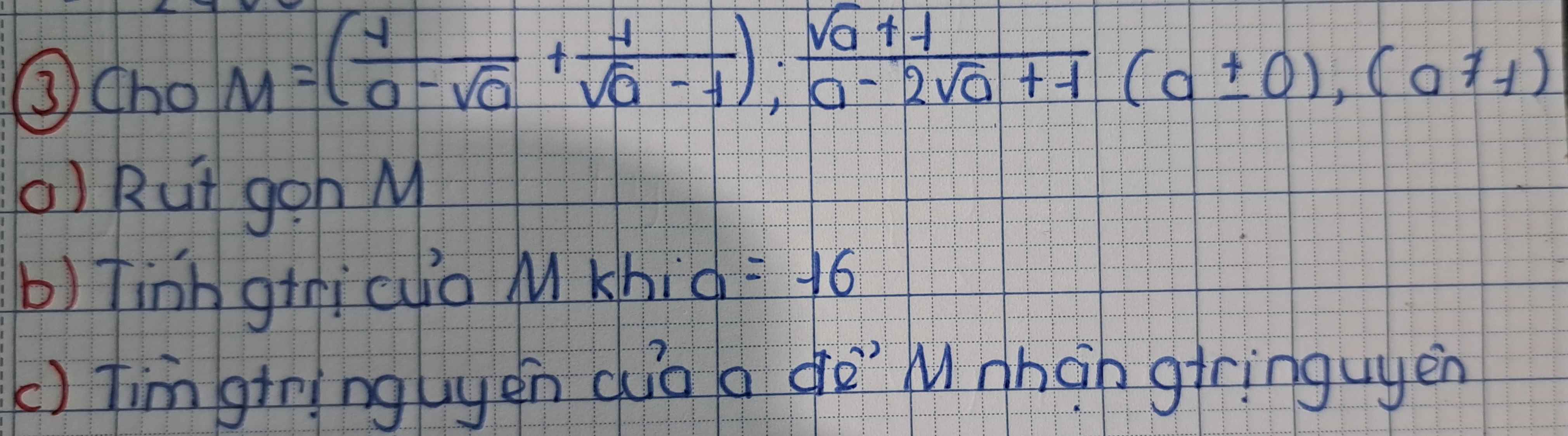
giúp mình vs mình đg cần gấp