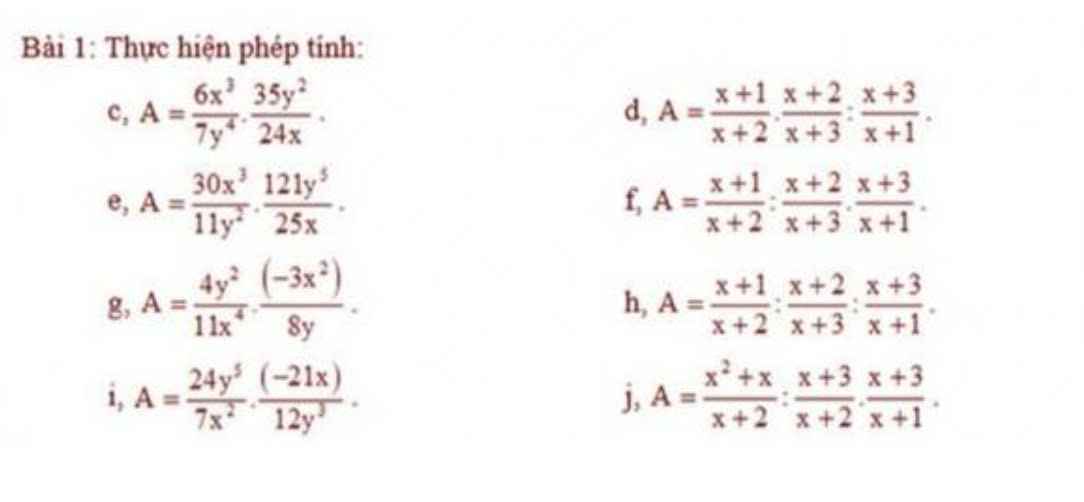c: \(A=\dfrac{6x^3}{7y^4}\cdot\dfrac{35y^2}{24x}=\dfrac{6x^3}{24x}\cdot\dfrac{35y^2}{7y^4}=\dfrac{x^2}{4}\cdot\dfrac{5}{y^2}=\dfrac{5x^2}{4y^2}\)
e: \(A=\dfrac{30x^3}{11y^2}\cdot\dfrac{121y^5}{25x}=\dfrac{30x^3}{25x}\cdot\dfrac{121y^5}{11y^2}=\dfrac{6x^2}{5}\cdot11y^3=\dfrac{66x^2y^3}{5}\)
g: \(A=\dfrac{4y^2}{11x^4}\cdot\dfrac{-3x^2}{8y}=\dfrac{4y^2}{8y}\cdot\dfrac{-3x^2}{11x^4}\)
\(=\dfrac{y}{2}\cdot\dfrac{-3}{11x^2}=\dfrac{-3y}{22x^2}\)
i: \(A=\dfrac{24y^5}{7x^2}\cdot\dfrac{-21x}{12y^3}=\dfrac{24y^4}{12y^3}\cdot\dfrac{-21x}{7x^2}=\dfrac{2y\cdot\left(-3\right)}{x}=\dfrac{-6y}{x}\)
f: \(A=\dfrac{x+1}{x+2}:\dfrac{x+2}{x+3}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{x+1}{x+2}\cdot\dfrac{x+3}{x+2}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{\left(x+3\right)^2}{\left(x+2\right)^2}\)
h: \(A=\dfrac{x+1}{x+2}:\dfrac{x+2}{x+3}:\dfrac{x+3}{x+1}\)
\(=\dfrac{x+1}{x+2}\cdot\dfrac{x+3}{x+2}\cdot\dfrac{x+1}{x+3}\)
\(=\dfrac{\left(x+1\right)^2}{\left(x+2\right)^2}\)
j: \(A=\dfrac{x^2+x}{x+2}:\dfrac{x+3}{x+2}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{x\left(x+1\right)}{x+2}\cdot\dfrac{x+2}{x+3}\cdot\dfrac{x+3}{x+1}\)
=x