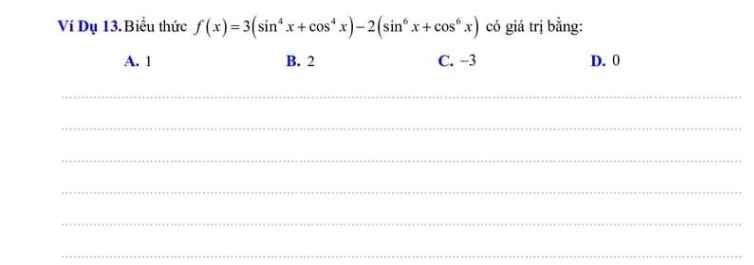Question

  giúp e bài này vs ạ

Answer 1

\(F\left(x\right)=3\cdot\left(sin^4x+cos^4x\right)-2\left(sin^6x+cos^6x\right)\)

\(=3\left[\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\right]-2\left[\left(sin^2x+cos^2\right)^3-3\cdot\left(sin^2x+cos^2x\right)\cdot sin^2x\cdot cos^2x\right]\)

\(=3\left[1-2\cdot sin^2x\cdot cos^2x\right]-2\left[1-3sin^2x\cdot cos^2x\right]\)

\(=3-6\cdot sin^2x\cdot cos^2x-2+6\cdot sin^2x\cdot cos^2x\)

=3-2=1

=>Chọn A

Answer 2

A

Answer 3

Ta có:

+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.

+ sin4x + cos4x = 1 - 3sin2x.cos2x.

Do đó

A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.