\(a,P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\\ =\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\left(2\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)\\ =\sqrt{x}\left(\sqrt{x}-1\right)-2\sqrt{x}-1+2\sqrt{x}+2\\ =x-\sqrt{x}+1\)
b)
\(P=7\\ =>x-\sqrt{x}+1=7\\ < =>>x-\sqrt{x}+1-7=0\\ < =>x-\sqrt{x}-6=0\\ < =>\left(x-3\sqrt{x}\right)+\left(2\sqrt{x}-6\right)=0\\ < =>\sqrt{x}\left(\sqrt{x}-3\right)+2\left(\sqrt{x}-3\right)=0\\ < =>\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)=0\\ < =>\left[{}\begin{matrix}\sqrt{x}=-2\text{(vô lý)}\\\sqrt{x}=3\end{matrix}\right.\\ < =>x=9\left(tm\right)\)
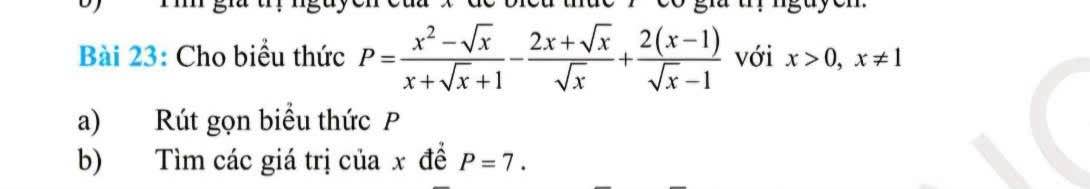


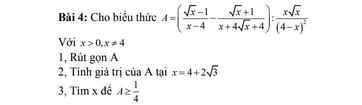 Mn giúp e với
Mn giúp e với 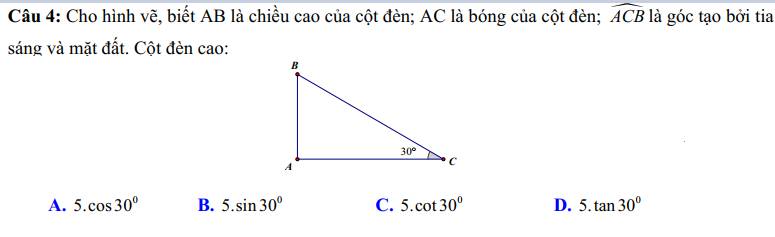
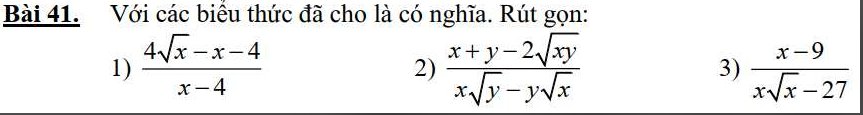 giúp e gấp với ạ, e cảm ơn
giúp e gấp với ạ, e cảm ơn

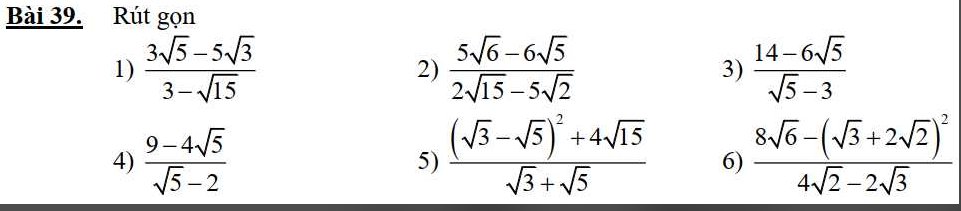 làm rõ ra giúp e ạ, e cảm ơn
làm rõ ra giúp e ạ, e cảm ơn


