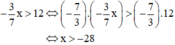a.\(5x-2=2x+7\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\)
b.\(\dfrac{4x-1}{3}-\dfrac{x+3}{2}=\dfrac{x-5}{6}\)
\(\Leftrightarrow\dfrac{2\left(4x-1\right)-3\left(x+3\right)}{6}=\dfrac{x-5}{6}\)
\(\Leftrightarrow2\left(4x-1\right)-3\left(x+3\right)=x-5\)
\(\Leftrightarrow8x-2-3x-9=x-5\)
\(\Leftrightarrow4x=6\)
\(\Leftrightarrow x=\dfrac{3}{2}\)
Vậy \(S=\left\{\dfrac{3}{2}\right\}\)
c.\(3x\left(x+2\right)-5\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(3x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{5}{3}\end{matrix}\right.\)
d.\(\dfrac{7}{x-3}-\dfrac{5}{x+3}=\dfrac{18}{x^2-9}\)
\(ĐK:x\ne\pm3\)
\(\Leftrightarrow\dfrac{7\left(x+3\right)-5\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{18}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow7\left(x+3\right)-5\left(x-3\right)=18\)
\(\Leftrightarrow7x+21-5x+15=18\)
\(\Leftrightarrow2x=-18\)
\(\Leftrightarrow x=-9\left(tm\right)\)
Vậy \(S=\left\{-9\right\}\)
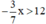. Ta có:
