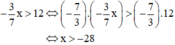Điều kiện: \(x\ne\pm2\)
\(\dfrac{x}{x-2}-\dfrac{x+3}{x+2}=\dfrac{4}{x^2-4}\\ \Leftrightarrow\dfrac{x\left(x+2\right)-\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow x^2+2x-x^2+2x-3x+6-4=0\\ \Leftrightarrow x=-2\)
Kết hợp điều kiện xác định, ta thấy phương trình vô nghiệm.
\(\dfrac{x}{x-2}-\dfrac{x+3}{x+2}=\dfrac{4}{x^2-4}\left(x\ne\pm2\right)\\ \Leftrightarrow\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\\\Rightarrow x\left(x+2\right)-\left(x+3\right)\left(x-2\right)=4\\ \Leftrightarrow x^2+2x-\left(x^2-2x+3x-6\right)-4=0\\ \Leftrightarrow x^2+2x-x^2+2x-3x+6-4=0\\ \Leftrightarrow x+2\\ \Leftrightarrow x=-2\left(loại\right)\)
Vậy phương trình đã cho vô nghiệm.




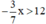 . Ta có:
. Ta có: