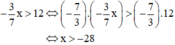\(\Leftrightarrow\dfrac{-3}{\left(x-1\right)\left(x+1\right)}-\dfrac{1}{x+1}=\dfrac{2}{\left(x-1\right)^2\cdot\left(x+1\right)}\)
=>-3(x-1)-(x-1)^2=2
=>-3x+3-x^2+2x-1=2
=>-x^2-x+2=2
=>-x^2-x=0
=>x(x+1)=0
=>x=0(nhận) hoặc x=-1(loại)
\(DKXD:x\ne\pm1\)
\(\Leftrightarrow\dfrac{2}{x^2\left(x-1\right)-\left(x-1\right)}-\dfrac{3}{1-x^2}+\dfrac{1}{x+1}=0\)
\(\Leftrightarrow\dfrac{2}{\left(x-1\right)^2\left(x+1\right)}-\dfrac{3}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+1}=0\)
\(\Leftrightarrow\dfrac{2-3\left(x-1\right)+1\left(x^2-2x+1\right)}{\left(x-1\right)^2\left(x+1\right)}=0\)
\(\Leftrightarrow2-3x+3+x^2-2x+1=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=3\left(n\right)\\x_2=2\left(n\right)\end{matrix}\right.\)
Vậy \(S=\left\{3;2\right\}\)
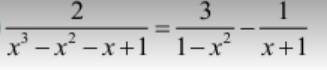
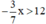. Ta có:
