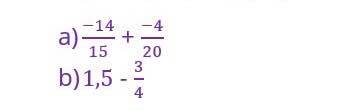\(\text{#idT60311}\)
`2.`
`a)`
Xét `\Delta AMB` và `\Delta AMC`:
\(\text{AB = AC (gt)}\)
\(\text{AM}\) chung
\(\text{MA = MB}\) `(` M là trung điểm của BC`)`
`=> \Delta AMB = \Delta AMC (c-c-c)`
`b)`
Vì `\Delta AMB = \Delta AMC (a)`
`=>`\(\widehat{\text{BAM}}=\widehat{\text{CAM}}\left(\text{2 góc tương ứng}\right)\)
`c)`
Vì `\Delta AMB = \Delta AMC (b)`
`=>`\(\widehat{\text{AMB}}=\widehat{\text{AMC}}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>`\(\widehat{\text{AMB}}+\widehat{\text{AMC}}=180^0\)
`=>`\(\widehat{\text{AMB}}=\widehat{\text{AMC}}=\dfrac{180}{2}=90^0\)
`=>`\(\text{AM }\bot\text{ BC}\).
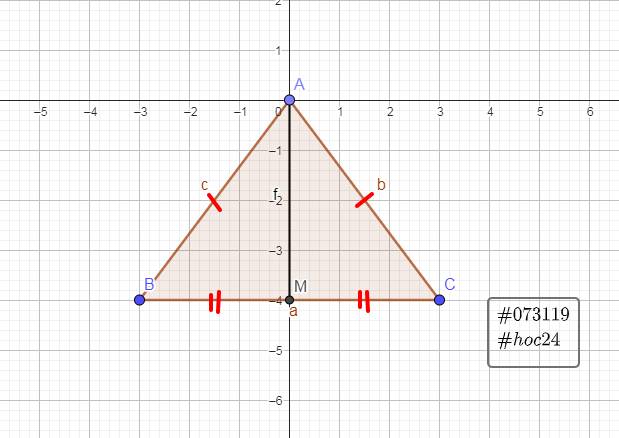
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: ΔAMB=ΔAMC
=>\(\widehat{BAM}=\widehat{CAM}\)
c: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
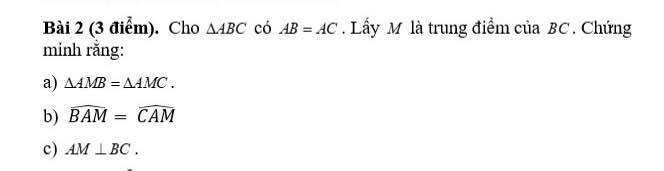






 giải hộ bài 5 có hình + cách giải với ạ
giải hộ bài 5 có hình + cách giải với ạ