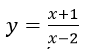Câu 12:
Để hàm số $y$ đồng biến trên từng khoảng xác định thì:
\(y'=\frac{m+1}{(x+1)^2}> 0, \forall x\in (-\infty;-1)\cup (-1;+\infty)\)
\(\Leftrightarrow m> -1\)
Đáp án B.
Câu 13:
$y=x^3-3m^2x$
$y'=3x^2-3m^2$. Để $y$ đồng biến trên $\mathbb{R}$ thì $y'\geq 0, \forall x\in\mathbb{R}$
$\Leftrightarrow x^2\geq m^2, \forall x\in\mathbb{R}$
$\Leftrightarrow m^2\leq min (x^2)=0$. Điều này xảy ra khi $m=0$
Đáp án D.
Câu 11:
Hàm số không xác định tại $2$ nên mẫu là $x-2$. Loại đáp án B.
\(\lim\limits_{x\to \infty}y=2\) nên loại đáp án C
\(\lim\limits_{x\to 2-}y=-\infty\) nên chỉ có đáp án D đúng.
Câu 14:
$y'=\cos x-m$
Để $y$ nghịch biến trên $\mathbb{R}$ thì $y'\geq 0$ với mọi $x\in\mathbb{R}$
$\Leftrightarrow \cos x-m\leq 0,\forall x\in\mathbb{R}$
$\Leftrightarrow m\geq \cos x, \forall x\in\mathbb{R}$
$\Leftrightarrow m\geq \max (\cos x), \forall x\in\mathbb{R}$
$\Rightarrow m\geq 1$
Đáp án D.
Câu 15:
\(y'=x^2+2(m+1)x-(m+1)\)
$y$ đồng biến trên $\mathbb{R}$ thì $y'=x^2+2(m+1)x-(m+1)\geq 0, \forall x\in\mathbb{R}$
\(\Leftrightarrow \left\{\begin{matrix} 1>0\\ \Delta'=(m+1)^2+(m+1)\leq 0\end{matrix}\right.\)
\(\Leftrightarrow -2\leq m\leq -1\)
Đáp án B
Câu 16:
\(y'=-3x^2+6x+3m=3(-x^2+2x+m)\)
Để $y$ nghịch biến trên $(0;+\infty)$ thì $y'\leq 0, \forall x\in (0;+\infty)$
$\Leftrightarrow -x^2+2x+m\leq 0, \forall x\in (0;+\infty)$
$\Leftrightarrow m\leq x^2-2x, \forall x\in (0;+\infty)$
$\Leftrightarrow m\leq \min (x^2-2x), \forall x\in (0;+\infty)$
Hay $m\leq -1$
Đáp án B.
Câu 17:
\(y'=\frac{-(m^2+1)}{(x-m)^2}<0\) với mọi $x$ thuộc TXĐ và $m\in\mathbb{R}$
Do đó hàm $y$ nghịch biến trên từng khoảng xác định với mọi $m\in\mathbb{R}$
Đáp án C.
Câu 18:
Để hàm số $y$ đồng biến trên $(2;+\infty)$ thì:\(y'=\frac{-(m+2)}{(x-m)^2}>0, \forall x\in (2;+\infty)\)
\(\Leftrightarrow \left\{\begin{matrix} -(m+2)>0\\ m\neq x, \forall x\in (2;+\infty)\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m< -2\\ m\in (-\infty;2]\end{matrix}\right.\)
\(\Leftrightarrow m\in (-\infty;-2)\)
Đáp án D.