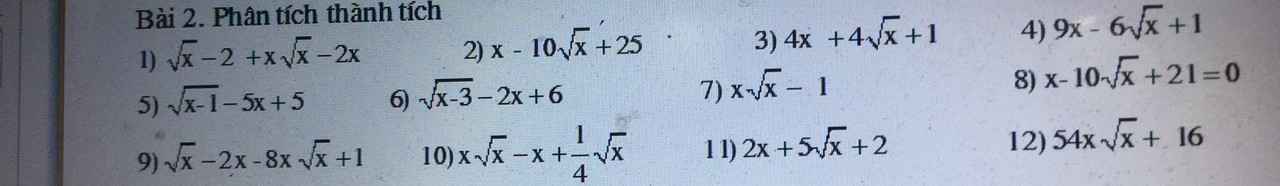1.
\(\sqrt{x}-2+x\sqrt{x}-2x=(\sqrt{x}-2)+(x\sqrt{x}-2x)=(\sqrt{x}-2)+x(\sqrt{x}-2)\)
\(=(\sqrt{x}-2)(1+x)\)
2.
\(x-10\sqrt{x}+25=(\sqrt{x})^2-2.5.\sqrt{x}+5^2=(\sqrt{x}-5)^2\)
3.
\(4x+4\sqrt{x}+1=(2\sqrt{x})^2+2.2\sqrt{x}+1=(2\sqrt{x}+1)^2\)
4.
\(9x-6\sqrt{x}+1=(3\sqrt{x})^2-2.3\sqrt{x}+1=(3\sqrt{x}-1)^2\)
5.
\(\sqrt{x-1}-5x+5=\sqrt{x-1}-5(x-1)=\sqrt{x-1}(1-5\sqrt{x-1})\)
6.
\(\sqrt{x-3}-2x+6=\sqrt{x-3}-2(x-3)=\sqrt{x-3}(1-2\sqrt{x-3})\)
7.
\(x\sqrt{x}-1=(\sqrt{x})^3-1^3=(\sqrt{x}-1)(x+\sqrt{x}+1)\)
8.
\(x-10\sqrt{x}+21=x-3\sqrt{x}-(7\sqrt{x}-21)\)
\(=\sqrt{x}(\sqrt{x}-3)-7(\sqrt{x}-3)=(\sqrt{x}-7)(\sqrt{x}-3)\)
9.
\(\sqrt{x}-2x-8x\sqrt{x}+1=(\sqrt{x}-2x)+(1-8x\sqrt{x})\)
\(=\sqrt{x}(1-2\sqrt{x})+[1^3-(2\sqrt{x})^3]=\sqrt{x}(1-2\sqrt{x})+(1-2\sqrt{x})(1+2\sqrt{x}+4x)\)
\(=(1-2\sqrt{x})(\sqrt{x}+1+2\sqrt{x}+4x)\)
\(=(1-2\sqrt{x})(4x+3\sqrt{x}+1)\)
10.
\(x\sqrt{x}-x+\frac{1}{4}\sqrt{x}=\sqrt{x}(x-\sqrt{x}+\frac{1}{4})\)
\(=\sqrt{x}[(\sqrt{x})^2-2.\frac{1}{2}.\sqrt{x}+(\frac{1}{2})^2]=\sqrt{x}(\sqrt{x}-\frac{1}{2})^2\)
11.
\(2x+5\sqrt{x}+2=2x+4\sqrt{x}+\sqrt{x}+2=2\sqrt{x}(\sqrt{x}+2)+(\sqrt{x}+2)\)
\(=(2\sqrt{x}+1)(\sqrt{x}+2)\)
12.
\(54x\sqrt{x}+16=2(27x\sqrt{x}+8)=2[(3\sqrt{x})^3+2^3]\)
\(=2(3\sqrt{x}+2)(9x-6\sqrt{x}+4)\)
1) \(\sqrt{x}-2+x\sqrt{x}-2x=\left(\sqrt{x}-2\right)\left(1+x\right)\)
2) \(x-10\sqrt{x}+25=\left(\sqrt{x}-5\right)^2\)
3) \(4x+4\sqrt{x}+1=\left(2\sqrt{x}+1\right)^2\)
4) \(9x-6\sqrt{x}+1=\left(3\sqrt{x}-1\right)^2\)
5) \(\sqrt{x-1}-5x+5=\sqrt{x-1}\cdot\left(1-5\sqrt{x-1}\right)\)
6) \(\sqrt{x-3}-2x+6=\sqrt{x-3}\left(1-2\sqrt{x-3}\right)\)
7) \(x\sqrt{x}-1=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
8) \(x-10\sqrt{x}+21=\left(\sqrt{x}-7\right)\left(\sqrt{x}-3\right)\)
10) \(x\sqrt{x}-x+\dfrac{1}{4}\sqrt{x}=\sqrt{x}\cdot\left(x-\sqrt{x}+\dfrac{1}{4}\right)=\sqrt{x}\cdot\left(\sqrt{x}-\dfrac{1}{2}\right)^2\)
11) \(2x+5\sqrt{x}+2=\left(2\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\)
12) \(54x\sqrt{x}+16=2\left(27x\sqrt{x}+8\right)=2\left(3\sqrt{x}+2\right)\left(9x-6\sqrt{x}+4\right)\)