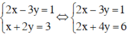 (Nhân cả hai vế phương trình thứ hai với 2)
(Nhân cả hai vế phương trình thứ hai với 2)
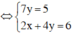 (Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
(Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
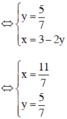
Vậy hệ phương trình có nghiệm 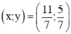
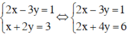 (Nhân cả hai vế phương trình thứ hai với 2)
(Nhân cả hai vế phương trình thứ hai với 2)
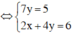 (Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
(Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
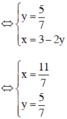
Vậy hệ phương trình có nghiệm 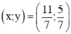
a, giải phương trình : 4x²+√2x+3=8x+1
B, giải hệ phương trình :
{√x+y+1+(x+2y)=4(x+y) ²+√3*√x+y
X-4y-3=(2y)²-√2-x²
Giải hệ phương trình :
\(\left\{{}\begin{matrix}\sqrt{3+2x^2y-x^4y^2}+x^4\left(1-2x^2\right)=y^2\\1+\sqrt{1+\left(x-y\right)^2}=x^3\left(x^3-x+2y^2\right)\end{matrix}\right.\)
1, Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^3-y^3-8x=3y\\x^2-3y^2=6\end{matrix}\right.\)
Giải hệ phương trình:
\(\hept{\begin{cases}2y^3+y+2x\sqrt{1-x}=3\sqrt{1-x}\\\sqrt{2y^2+1}-y=2-x\end{cases}}\)
Cho hệ phương trình x + y + 1 + 1 = 4 x + y 2 + 3 . x + y 2 x - y = 3 2 .Giả sử (x;y) là cặp nghiệm của hệ phương trình. Khi đó, A = 9x2 – 12y + 1 bằng
A. 3
B. 9
C. 4
D. 7
giải hệ phương trình
\(\hept{\begin{cases}x^2\\x^3+3y^2+5x-12=\left(12-y\right)\sqrt{3-x}\end{cases}+y^2+1=2\left(xy-x+y\right)}\)
Giải hệ phương trình
X^2 -x +√x = Xy + √(y+1)
2x^3 +1 = x√(4x^2 +5y^2-5) +9y
Giải hệ phương trình : \(\hept{\begin{cases}x+\frac{5xy}{x^2+y^2}=2\left(y+1\right)\\\left(x-1\right)^2=y\left(3-5y\right)\end{cases}}\)
giải hệ phương trình \(\hept{\begin{cases}\sqrt{3+x^2}+2\sqrt{x+3}=5+\sqrt{y+3}\\\sqrt{3+y^2}+2\sqrt{y+3}=5+\sqrt{x+3}\end{cases}}\)
Giải hệ phương trình
\(\left\{{}\begin{matrix}x^2y+2y+x=4xy\\\dfrac{1}{x^2}+\dfrac{1}{xy}+\dfrac{x}{y}=3\end{matrix}\right.\)