3:
ĐKXĐ: x>=0; x<>1
a: \(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0+1=1\)
=>\(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
mà 2>0
nên \(P=\dfrac{2}{x+\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ
Đúng 2
Bình luận (1)
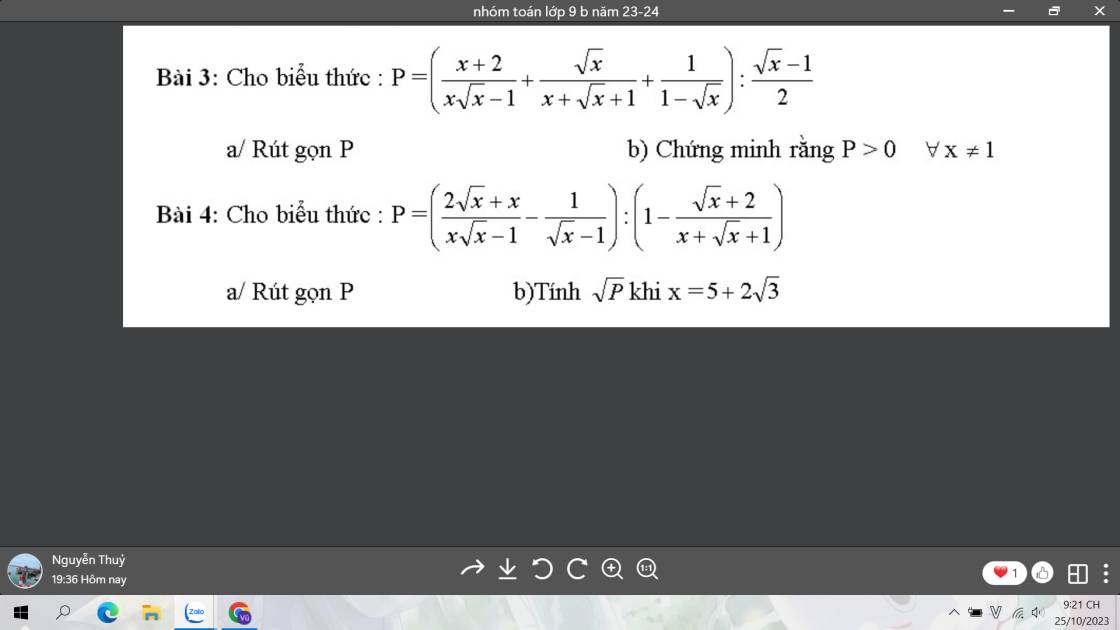 giải giúp mik bài 3 nha mn <3
giải giúp mik bài 3 nha mn <3
