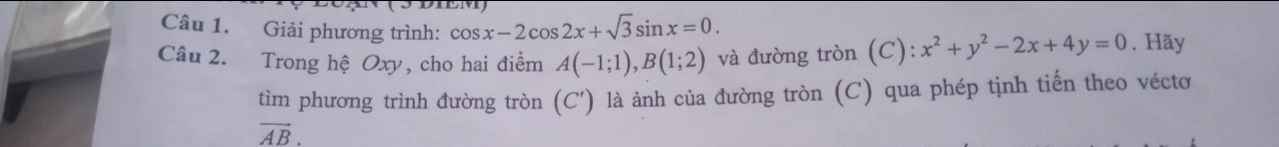1.
\(cosx-2cos2x+\sqrt{3}sinx=0\)
\(\Leftrightarrow cosx+\sqrt{3}sinx=2cos2x\)
\(\Leftrightarrow\dfrac{1}{2}cosx+\dfrac{\sqrt{3}}{2}sinx=cos2x\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{3}\right)=cos2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x-\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{3}+k2\pi\\x=\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
2.
\(\overrightarrow{AB}=\left(2;1\right)\)
Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=\sqrt{1^2+\left(-2\right)^2}=\sqrt{5}\)
Gọi \(I'\left(x';y'\right)\) và R' lần lượt là tâm và bán kính của (C')
\(\Rightarrow\left\{{}\begin{matrix}R'=R=\sqrt{5}\\T_{\overrightarrow{AB}}\left(I\right)=I'\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x'=1+2=3\\y'=-2+1=-1\end{matrix}\right.\)
\(\Rightarrow I'\left(3;-1\right)\)
Phương trình (C') có dạng:
\(\left(x-3\right)^2+\left(y+1\right)^2=5\)