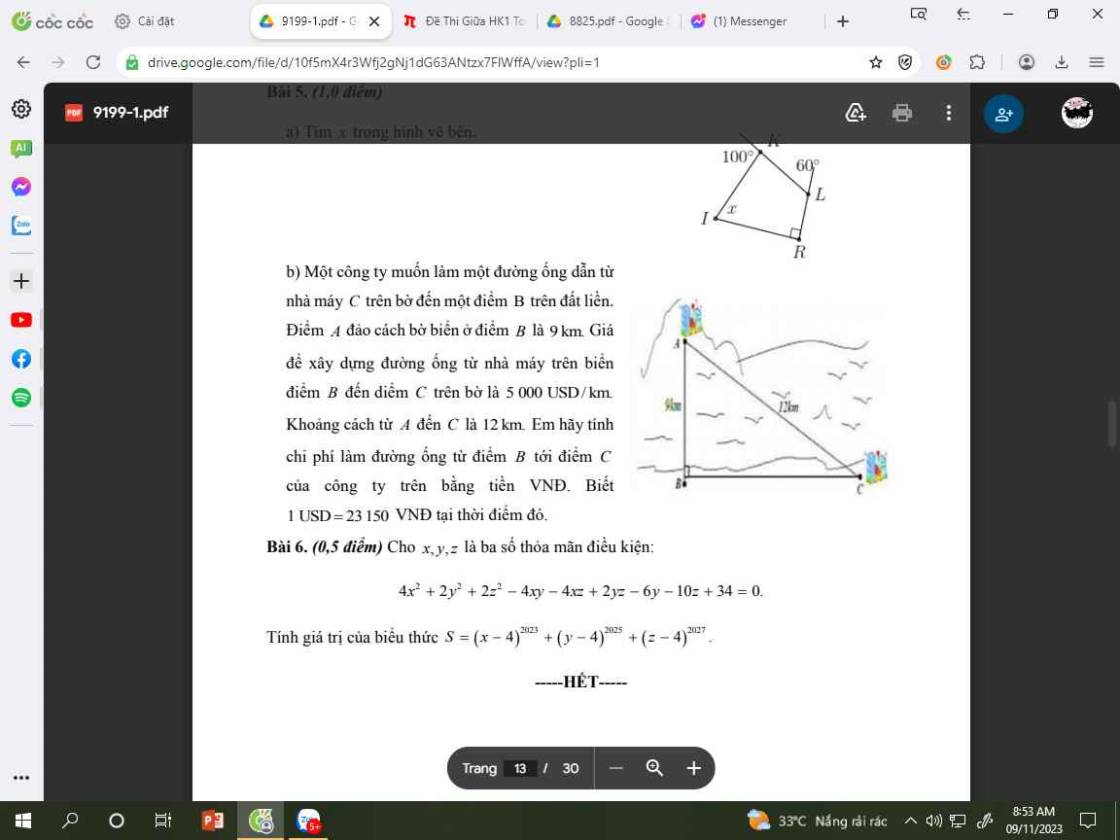
Bài 6: Ta có:
\(4x^2+2y^2+2z^2-4xy-4xz+2yz-6y-10z+34=0\)
\(\Leftrightarrow4x^2+y^2+z^2-4xy-4xz+2yz+y^2-6y+9+z^2-10z+25=0\)
\(\Leftrightarrow\left[\left(2x\right)^2+y^2+z^2-2\cdot2x\cdot y-2\cdot2x\cdot z+2\cdot y\cdot z\right]+\left(y^2-6y+9\right)+\left(z^2-10z+25\right)=0\)
\(\Leftrightarrow\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)
Mà: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2\ge0\forall x,y,z\)
Mặt khác: \(\left(2x-y-z\right)^2+\left(y-3\right)^2+\left(z-5\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y-z=0\\y-3=0\\z-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3-5=0\\y=3\\z=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=8\\y=3\\z=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\\z=5\end{matrix}\right.\)
Thay vào S ta có:
\(S=\left(4-4\right)^{2023}+\left(3-4\right)^{2025}+\left(5-4\right)^{2027}=0-1+1=0\)
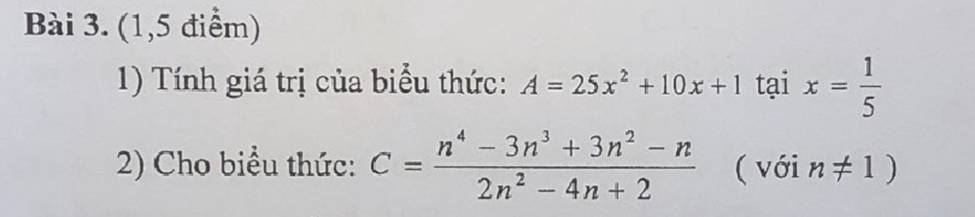Giải dùm mình với ạ! Mình cần gấp
