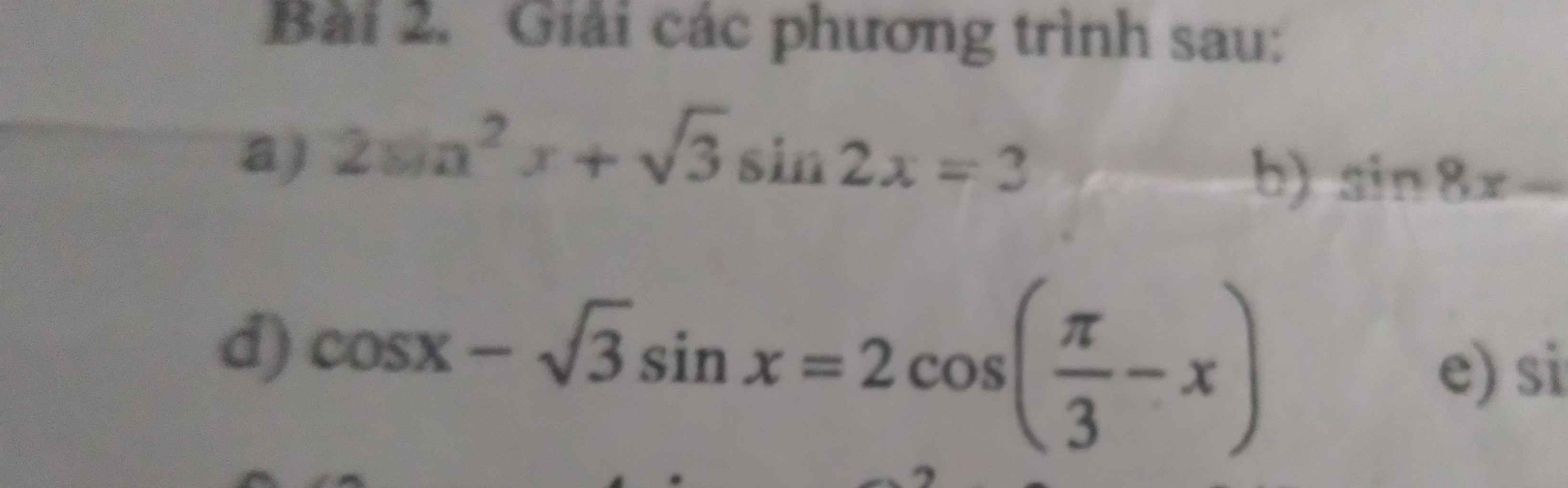a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
d, cosx - \(\sqrt{3}\)sinx = 2cos\(\left(\dfrac{\pi}{3}-x\right)\)
⇔ \(2cos\left(x+\dfrac{\pi}{3}\right)=2cos\left(x-\dfrac{\pi}{3}\right)\)
⇔ \(cos\left(x+\dfrac{\pi}{3}\right)-cos\left(x-\dfrac{\pi}{3}\right)\) = 0
⇔ \(-2sinx.sin\dfrac{\pi}{3}=0\)
⇔ sinx = 0
⇔ x = kπ , k ∈ Z
Sử dụng các công thức sau :
\(cos\left(x+\dfrac{\pi}{3}\right)=cosx.cos\dfrac{\pi}{3}-sinx.sin\dfrac{\pi}{3}=\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx\)
\(cosa-cosb=-2sin\dfrac{a+b}{2}.sin\dfrac{a-b}{2}\)