3.
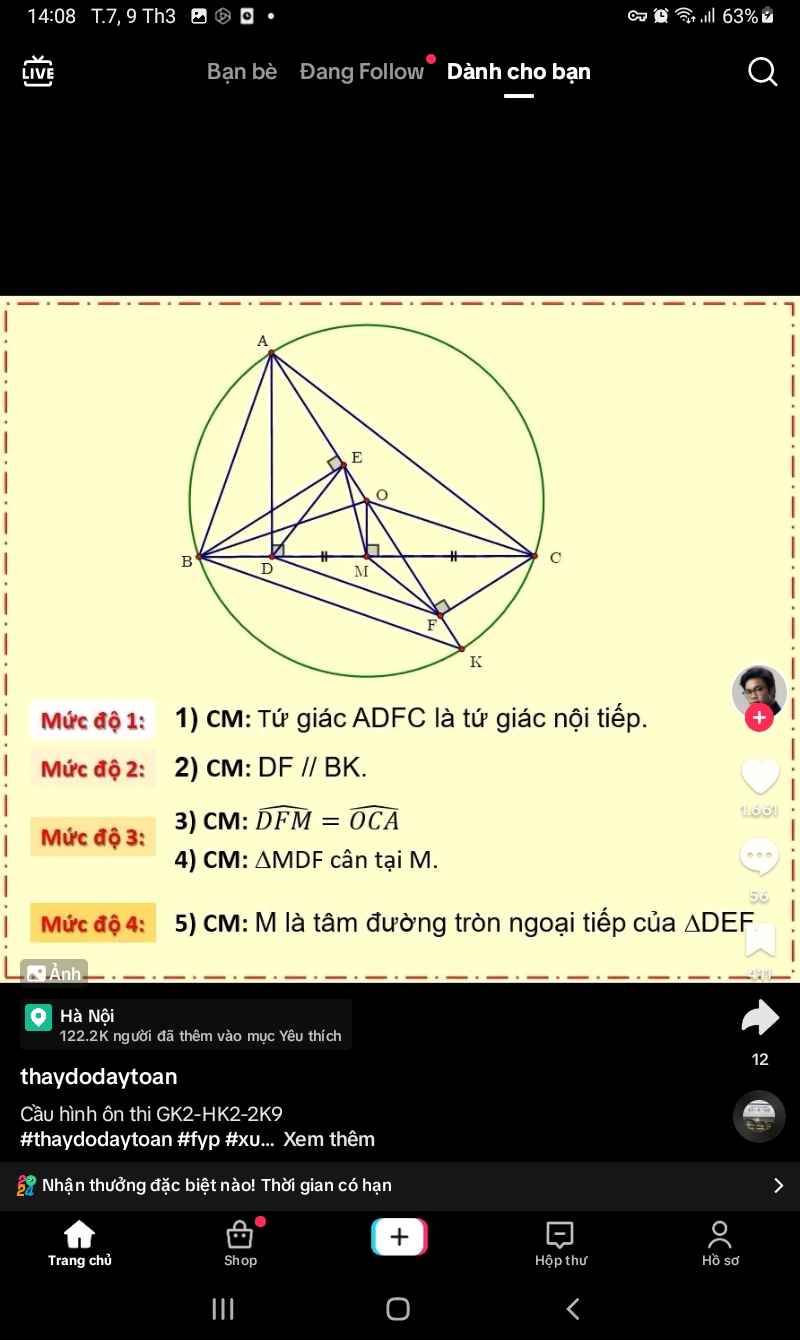
Do M và F cùng nhìn OC dưới 1 góc vuông \(\Rightarrow OCFM\) nội tiếp
\(\Rightarrow\widehat{OCM}=\widehat{OFM}\) (cùng chắn OM)
D và F cùng nhìn AC dưới 1 góc vuông \(\Rightarrow ADFC\) nội tiếp
\(\Rightarrow\widehat{AFD}=\widehat{ACD}\)
Hay \(\widehat{OFM}+\widehat{DFM}=\widehat{OCM}+\widehat{OCA}\)
\(\Rightarrow\widehat{DFM}=\widehat{OCA}\)
4.
\(OA=OC=R\Rightarrow\widehat{OCA}=\widehat{OAC}\) (hai góc đáy tam giác cân)
\(\widehat{OAC}=\widehat{KBC}\) (cùng chắn CK)
\(\widehat{KBC}=\widehat{MDF}\) (đồng vị)
\(\Rightarrow\widehat{DFM}=\widehat{DMF}\)
\(\Rightarrow\Delta DFM\) cân tại M
5.
Từ trên ta suy ra \(MD=MF\)
E và M cùng nhìn OB dưới 1 góc vuông \(\Rightarrow OMBE\) nội tiếp
\(\Rightarrow\widehat{MEO}=\widehat{MBO}\) (cùng chắn OM)
OB=OC=R nên OBC cân tại O \(\Rightarrow\widehat{MBO}=\widehat{MCO}\)
Mà \(\widehat{MCO}=\widehat{MFO}\) (cùng chắn MO của đường tròn nội tiếp OCFM)
\(\Rightarrow\widehat{MEO}=\widehat{MFO}\)
\(\Rightarrow\Delta MEF\) cân tại M
\(\Rightarrow ME=MF\Rightarrow MD=ME=MF\)
Hay M là tâm đường tròn ngoại tiếp DEF