giải chi tiết giúp mình với ạ
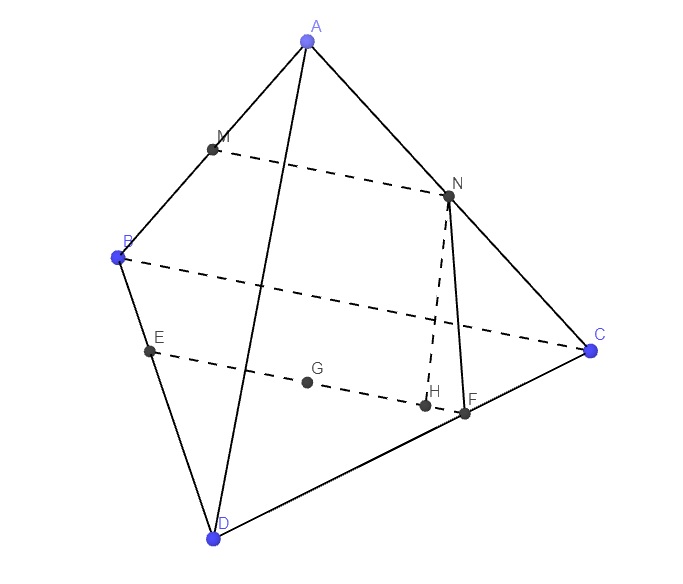
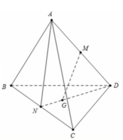
cho tứ diện ABCD (đáy BCD)gọi M,N lần lượt là trung điểm của AB,AC và G là trọng tâm của tam giác BCD
khẳng định sau là đúng hay sai
a) giả sử E,F lần lượt là giao điểm của mặt phẳng (MNG) với các đường thẳng BD và CD. Khi đó EF=\(\dfrac{2}{3}MN\)
b) giả sử ABCD là tứ diện đều có cạnh bằng 6 gọi E,F lần lượt là giao điểm của mặt phẳng (MNG) với các đường thẳng BD và CD. Khi đó diện tích tứ giác MNFE bằng \(\dfrac{21\sqrt{3}}{4}\)
a.
Từ giả thiết ta có MN là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}MN||AB\\MN=\dfrac{1}{2}AB\end{matrix}\right.\)
Qua G kẻ đường thẳng song song AB cắt BD, CD tại E và F
Gọi I là trung điểm BC, theo định lý Talet và tính chất trọng tâm:
\(\dfrac{EF}{AB}=\dfrac{DG}{DI}=\dfrac{2}{3}\Rightarrow EF=\dfrac{2}{3}AB=\dfrac{2}{3}.2MN=\dfrac{4}{3}MN\)
b.
Theo cm câu a ta có MN song song EF, đồng thời ABCD là tứ diện đều nên MNFE là hình thang cân
\(MN=\dfrac{1}{2}AB=3\) ; \(EF=\dfrac{4}{3}MN=4\)
Từ N kẻ NH vuông góc EF
\(\Rightarrow2HF=EF-MN=\dfrac{4}{3}MN-MN=\dfrac{1}{3}MN=\dfrac{1}{6}AB=1\)
\(\Rightarrow HF=\dfrac{1}{2}\)
\(NC=\dfrac{1}{2}AC=3\) ; \(CF=\dfrac{1}{3}CD=2\)
Áp dụng định lý hàm cosin:
\(NF=\sqrt{NC^2+CF^2-2NC.CF.cos60^0}=\sqrt{7}\)
\(\Rightarrow NH=\sqrt{NF^2-HF^2}=\dfrac{3\sqrt{3}}{2}\)
\(S=\dfrac{1}{2}\left(MN+EF\right).NH=\dfrac{21\sqrt{3}}{4}\)