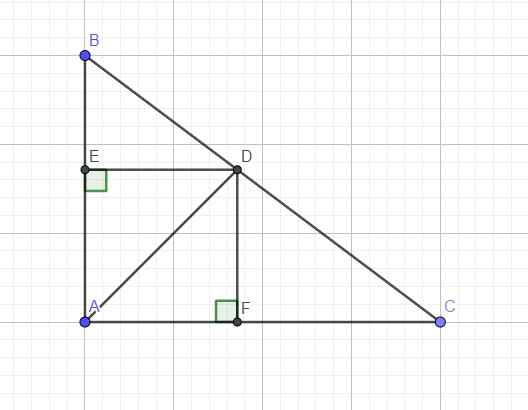
Từ D lần lượt kẻ DE vuông góc AB và DF vuông góc AC
\(\Rightarrow DE=DF\) (theo giả thiết)
\(\Rightarrow\)Tứ giác AEDF là hình vuông (có 3 góc vuông và 2 cạnh kề bằng nhau)
\(\Rightarrow AD\) là đường chéo đồng thời là phân giác góc A
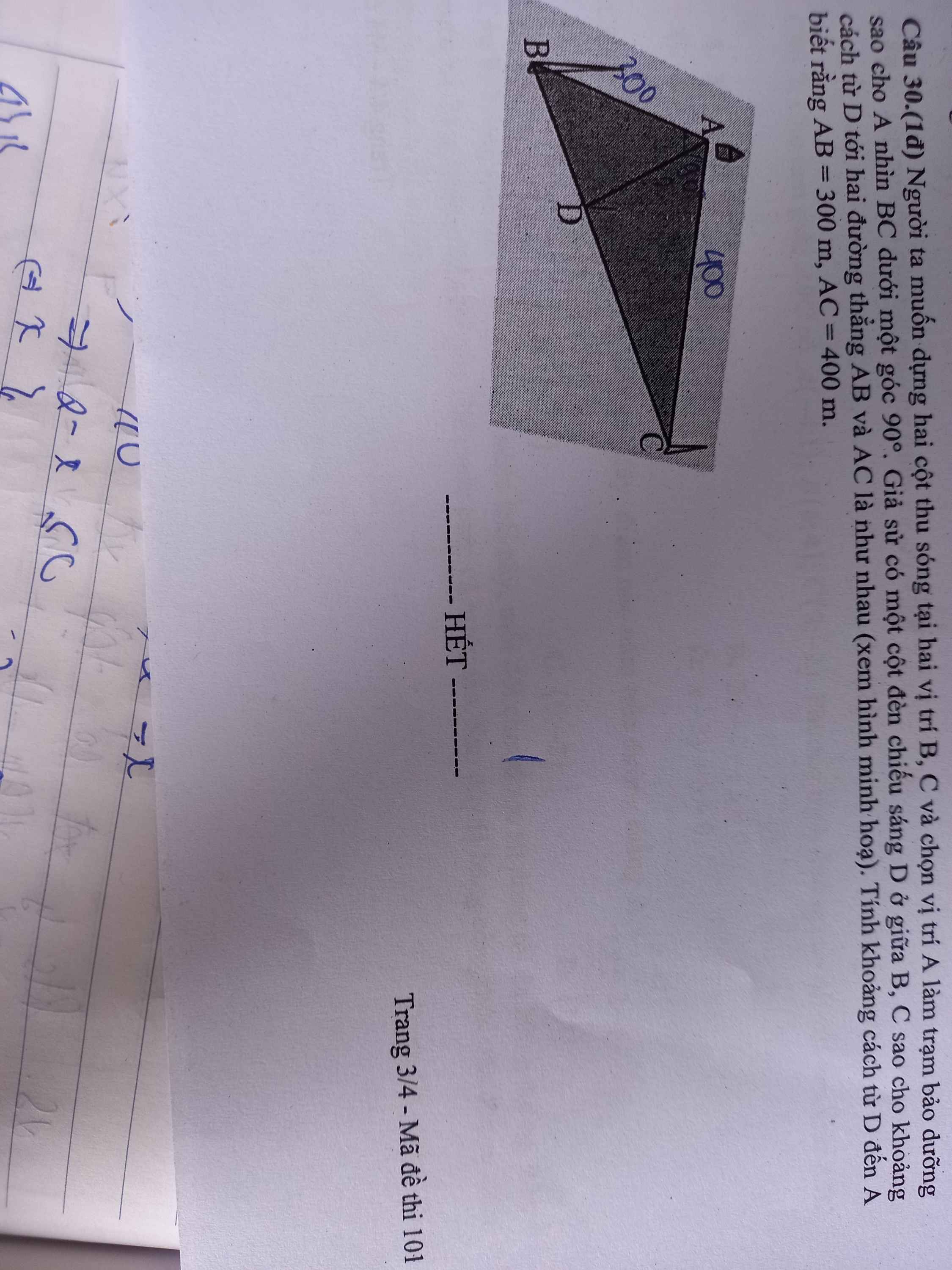
\(BC=\sqrt{AB^2+AC^2}=500\left(m\right)\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DC}{AC}\Leftrightarrow\dfrac{BD}{300}=\dfrac{500-BD}{400}\Rightarrow BD=\dfrac{1500}{7}\left(m\right)\)
Áp dụng Talet cho tam giác ABC:
\(\dfrac{BD}{BC}=\dfrac{DE}{AC}\Rightarrow DE=\dfrac{BD.AC}{BC}=\dfrac{1200}{7}\left(m\right)\)
\(\Rightarrow AD=DE\sqrt{2}\approx242,44\left(m\right)\)
Đúng 1
Bình luận (0)