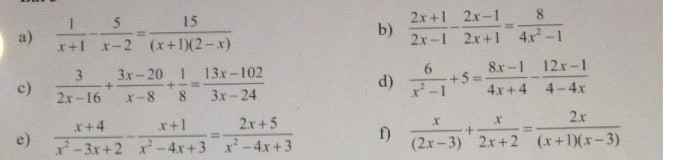c: ĐKXĐ: x<>8
\(\dfrac{3}{2x-16}+\dfrac{3x-20}{x-8}+\dfrac{1}{8}=\dfrac{13x-102}{3x-24}\)
=>\(\dfrac{9}{6\left(x-8\right)}+\dfrac{18x-120}{6\left(x-8\right)}-\dfrac{26x-204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{18x-111-26x+204}{6\left(x-8\right)}=\dfrac{-1}{8}\)
=>\(\dfrac{-8x+93}{6x-48}=\dfrac{-1}{8}\)
=>\(\dfrac{8x-93}{6x-48}=\dfrac{1}{8}\)
=>8(8x-93)=6x-48
=>64x-744-6x+48=0
=>58x=696
=>x=12
d: ĐKXĐ: x<>1; x<>-1
\(\dfrac{6}{x^2-1}+5=\dfrac{8x-1}{4x+4}+\dfrac{12x-1}{4x-4}\)
=>\(\dfrac{24}{4\left(x-1\right)\left(x+1\right)}+\dfrac{20\left(x^2-1\right)}{4\left(x-1\right)\left(x+1\right)}=\dfrac{\left(8x-1\right)\left(x-1\right)+\left(12x-1\right)\left(x+1\right)}{4\left(x-1\right)\left(x+1\right)}\)
=>8x^2-9x+1+12x^2+12x-x-1=24+20x^2-20
=>20x^2+2x=20x^2+4
=>2x=4
=>x=2(loại)