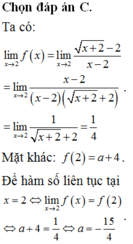Các câu hỏi tương tự
Cho hàm số y f(x)
2
x
+
m
x
-
1
. Tính tổng các giá trị của tham số m để
m
a
x
[
2
;
3
]
f...
Đọc tiếp
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2.
A. -4
B. -2
C. -1
D. -3
Cho hàm số y f(x)
2
x
+
m
x
-
1
. Tính tổng các giá trị của tham số m để
m
a
x
[
2
;
3
]...
Đọc tiếp
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2
A. -4
B. -2
C. -1
D. -3
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số y f(x) liên tục trên
ℝ
sao cho
m
a
x
x
∈
[
0
;
10
]
f
(
x
)
f(2) 4. Xét hàm số g(x)
f
x
3
+
x
-...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ sao cho m a x x ∈ [ 0 ; 10 ] f ( x ) = f(2) = 4. Xét hàm số g(x) = f x 3 + x - x 2 + 2 x + m . Giá trị của tham số m để m a x x ∈ [ 0 ; 2 ] g ( x ) = 8 là
A. 5
B. 4
C. -1
D. 3
Tìm giá trị thực của tham số m để hàm số
f
(
x
)
x
2
-
x
-
2...
Đọc tiếp
Tìm giá trị thực của tham số m để hàm số f ( x ) = x 2 - x - 2 x - 2 k h i x ≠ 2 m k h i x = 2 l i ê n t ụ c t ạ i x = 2
A.3
B.1
C.2
D.0
Giá trị của a để hàm số
y
f
(
x
)
x
-
1
-
1
x
2
-
3...
Đọc tiếp
Giá trị của a để hàm số y = f ( x ) = x - 1 - 1 x 2 - 3 x + 2 k h i x ≠ 2 2 a + 1 6 k h i x = 2 liên tục tại x = 2
A. 2
B. 1 2
C. 3
D. 1
Cho hàm số
f
(
x
)
2
x
2
+
3
x
-
2...
Đọc tiếp
Cho hàm số f ( x ) = 2 x 2 + 3 x - 2 x + 2 k h i x ≠ - 2 m 2 + m x - 8 k h i x = - 2
Tính tổng các giá trị tìm được của tham số m để hàm số liên tục tại x=-2
A.2
B.4
C.1
D.5
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Cho hàm số f(x)=x^2-4x+3. Có bao nhieu giá trị nguyên của tham số m để phương trình f^2(/x/)-(m-6)f(/x/)-m+5=0 có 6 nghiệm phân biệt