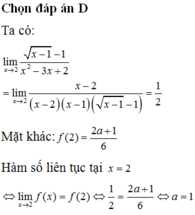Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
+
3
-
2
x...
Đọc tiếp
Cho hàm số f ( x ) = x + 3 - 2 x - 1 k h i x > 1 a x + 2 k h i x ⩽ 1 . Để hàm số liên tục tại x=1 thì a nhận giá trị là
A.1/2
B.1
C.-7/4
D.0
Biết
F
(
x
)
a
ln
|
x
-
1
|
+
b
ln
|
x
-
2
|
(
a
,
b
∈
Z
)
là một nguyên hàm của hàm số
f
(
x
)
x
+...
Đọc tiếp
Biết F ( x ) = a ln | x - 1 | + b ln | x - 2 | ( a , b ∈ Z ) là một nguyên hàm của hàm số f ( x ) = x + 1 ( x - 1 ) ( x - 2 ) . Giá trị của biểu thức b-a bằng
![]()
![]()
![]()
![]()
Cho hàm số y
(
m
-
1
)
x
3
-
3
(
m
+
2
)
x
2
-
6
(
m
+
2
)
x
+
1
. Tập giá trị của m để
y
≥
0
∀
x
∈
ℝ
là A. [3;+
∞
) B.
∅...
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 . Tập giá trị của m để y ' ≥ 0 ∀ x ∈ ℝ là
A. [3;+ ∞ )
B. ∅
C. [ 4 2 ;+ ∞ )
D. [1;+ ∞ )
Giá trị của tham số a để hàm số
y
f
(
x
)
x
+
2
-
2
x
-
2
...
Đọc tiếp
Giá trị của tham số a để hàm số y = f ( x ) = x + 2 - 2 x - 2 k h i x ≠ 2 a + 2 x k h i x = 2 liên tục tại x=2.
A. 1 4 .
B. 1.
C. - 15 4 .
D. 4.
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
(
0
a
≠
1
)
qua điểm I(2; 1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ( 0 < a ≠ 1 ) qua điểm I(2; 1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Cho hàm số y f(x)
2
x
+
m
x
-
1
. Tính tổng các giá trị của tham số m để
m
a
x
[
2
;
3
]
f...
Đọc tiếp
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2.
A. -4
B. -2
C. -1
D. -3
Cho hàm số y f(x)
2
x
+
m
x
-
1
. Tính tổng các giá trị của tham số m để
m
a
x
[
2
;
3
]...
Đọc tiếp
Cho hàm số y = f(x) = 2 x + m x - 1 . Tính tổng các giá trị của tham số m để m a x [ 2 ; 3 ] f ( x ) - m i n [ 2 ; 3 ] f ( x ) = 2
A. -4
B. -2
C. -1
D. -3
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Cho hàm số y f(x) có đạo hàm f(x). Hàm số y f(x) liên tục trên tập số thực và có bảng biến thiên như sau: Biết rằng f(-1)
10
3
, f(2) 6. Giá trị nhỏ nhất của hàm số g(x)
f
3
(
x
)
-
3
f
(
x
)
trên đoạn [-1;2] bằng A.
10
3
B.
820
27...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
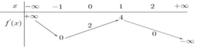
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198