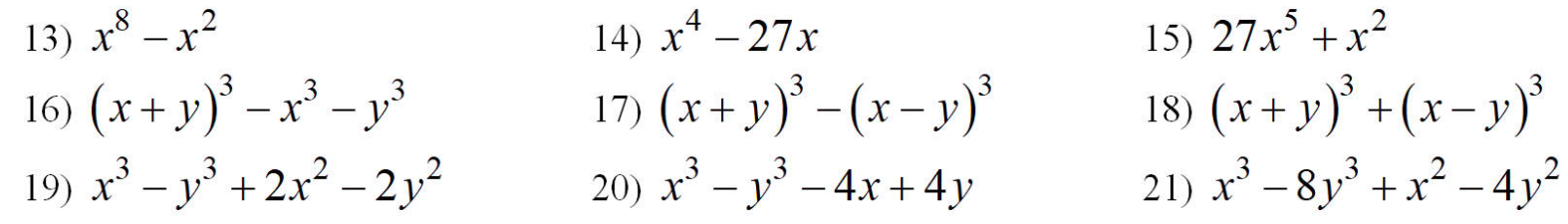13: \(x^8-x^2\)
\(=x^2\left(x^6-1\right)\)
\(=x^2\left(x^3-1\right)\left(x^3+1\right)\)
\(=x^2\left(x-1\right)\left(x+1\right)\left(x^2+x+1\right)\left(x^2-x+1\right)\)
16: \(\left(x+y\right)^3-x^3-y^3\)
\(=x^3+y^3+3xy\left(x+y\right)-x^3-y^3\)
=3xy(x+y)
19: \(x^3-y^3+2x^2-2y^2\)
\(=\left(x^3-y^3\right)+\left(2x^2-2y^2\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)+2\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2+2x+2y\right)\)
14: \(x^4-27x\)
\(=x\left(x^3-27\right)\)
\(=x\left(x-3\right)\left(x^2+3x+9\right)\)
17: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=\left(x+y-x+y\right)\left[\left(x+y\right)^2+\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\right]\)
\(=2y\left(x^2+2xy^2+y^2+x^2-y^2+x^2-2xy+y^2\right)\)
\(=2y\left(3x^2+y^2\right)\)
20: \(x^3-y^3-4x+4y\)
\(=\left(x^3-y^3\right)-\left(4x-4y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-4\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-4\right)\)
15: \(27x^5+x^2\)
\(=x^2\left(27x^3+1\right)\)
\(=x^2\left[\left(3x\right)^3+1^3\right]\)
\(=x^2\left(3x+1\right)\left(9x^2-3x+1\right)\)
18: \(\left(x+y\right)^3+\left(x-y\right)^3\)
\(=\left(x+y+x-y\right)\left[\left(x+y\right)^2-\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\right]\)
\(=2x\left(x^2+2xy+y^2-x^2+y^2+x^2-2xy+y^2\right)\)
\(=2x\left(3y^2+x^2\right)\)
21: \(x^3-8y^3+x^2-4y^2\)
\(=\left(x^3-8y^3\right)+\left(x^2-4y^2\right)\)
\(=\left(x-2y\right)\left(x^2+2xy+4y^2\right)+\left(x-2y\right)\left(x+2y\right)\)
\(=\left(x-2y\right)\cdot\left(x^2+2xy+4y^2+x+2y\right)\)