a:
Ta có: BE=BD+DE
CD=CE+ED
mà CE=BD
nên BE=CD
Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{ABE}=\widehat{ACD}\)(ΔABC cân tại A)
BE=CD
Do đó: ΔAEB=ΔADC
=>\(\widehat{EAB}=\widehat{DAC}\)
b: ΔBAC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC tại M
=>AM\(\perp\)DE tại M
ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xét ΔADE cân tại A có \(\widehat{DAE}=60^0\)
nên ΔADE đều
=>\(\widehat{ADE}=\widehat{AED}=60^0\)




 .Câu 7,8,9,10 ạ!!! mjk đag gấp
.Câu 7,8,9,10 ạ!!! mjk đag gấp
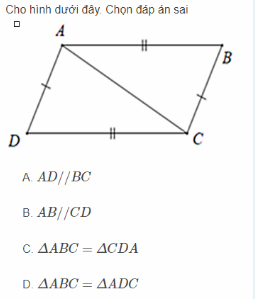 gấp gấp cứu e ạ
gấp gấp cứu e ạ
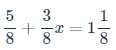
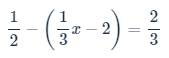
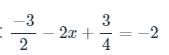
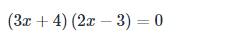
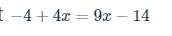
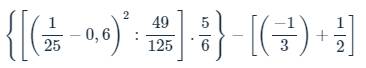 ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!
ghi kết quả thôi ạ , k phải trình bày ạ , e cần gấp ạ !!!!!

 giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em đang cần gấp ạ
giúp em với ạ em đang cần gấp ạ