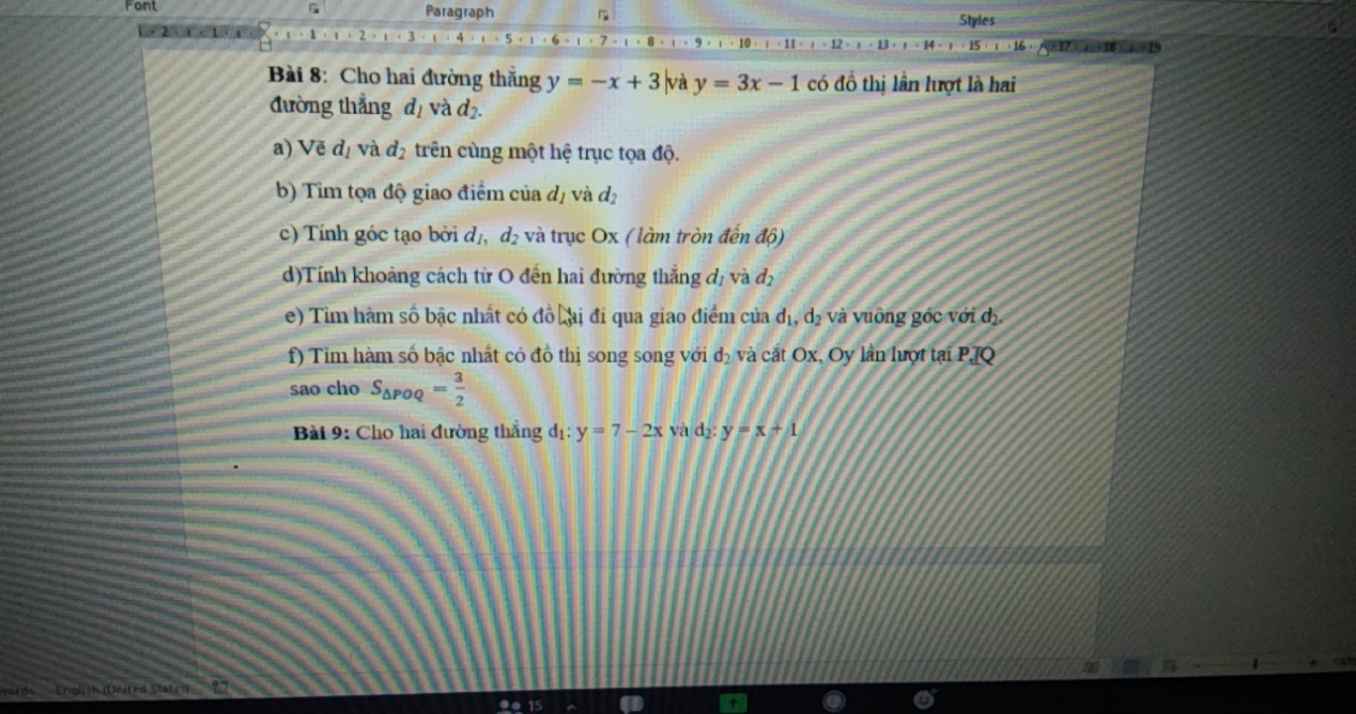
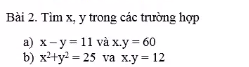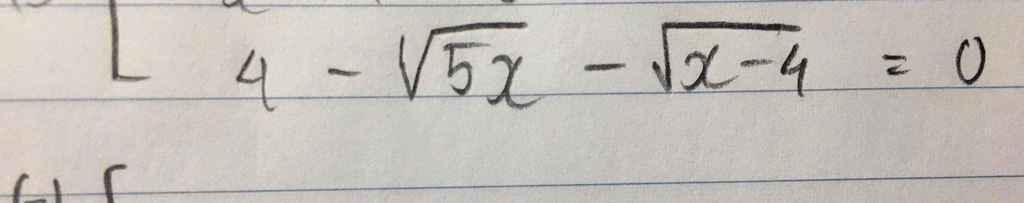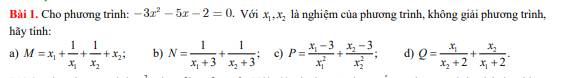Bài 2:
\(x^2+\left(m+2\right)x+2m=0\)
\(\text{Δ}=\left(m+2\right)^2-4\cdot1\cdot2m\)
\(=m^2+4m+4-8m=m^2-4m+4\)
\(=\left(m-2\right)^2>=0\forall m\)
=>Phương trình luôn có hai nghiệm x1;x2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(m+2\right)}{1}=-m-2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{2m}{1}=2m\end{matrix}\right.\)
\(2\cdot\left(x_1+x_2\right)+x_1x_2\)
\(=2\left(-m-2\right)+2m\)
=-2m-4+2m
=-4
=>Đây là hệ thức cần tìm
Bài 3:
a: Thay x=-2 vào phương trình, ta được:
\(\left(2m-1\right)\cdot\left(-2\right)^2+\left(m-3\right)\cdot\left(-2\right)-6m-2=0\)
=>\(4\left(2m-1\right)-2\left(m-3\right)-6m-2=0\)
=>8m-4-2m+6-6m-2=0
=>0=0
=>Phương trình luôn có nghiệm x=-2
b: TH1: m=1/2
Phương trình lúc này sẽ là:
\(\left(2\cdot\dfrac{1}{2}-1\right)\cdot x^2+\left(\dfrac{1}{2}-3\right)x-6\cdot\dfrac{1}{2}-2=0\)
\(\Leftrightarrow-\dfrac{5}{2}x-5=0\)
=>\(-\dfrac{5}{2}x=5\)
=>\(x=-5:\dfrac{5}{2}=-2\)
TH2: m<>1/2
\(\text{Δ}=\left(m-3\right)^2-4\left(2m-1\right)\left(-6m-2\right)\)
\(=m^2-6m+9+4\left(2m-1\right)\left(6m+2\right)\)
\(=m^2-6m+9+4\left(12m^2+4m-6m-2\right)\)
\(=m^2-6m+9+4\left(12m^2-2m-2\right)\)
\(=m^2-6m+9+48m^2-8m-8\)
\(=49m^2-14m+1=\left(7m-1\right)^2>=0\forall m\)
=>Phương trình luôn có hai nghiệm là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-\left(m-3\right)-\sqrt{\left(7m-1\right)^2}}{2\cdot\left(2m-1\right)}=\dfrac{-\left(m-3\right)-\left|7m-1\right|}{4m-2}\\x_2=\dfrac{-\left(m-3\right)+\sqrt{\left(7m-1\right)^2}}{2\left(2m-1\right)}=\dfrac{-\left(m-3\right)+\left|7m-1\right|}{4m-2}\end{matrix}\right.\)