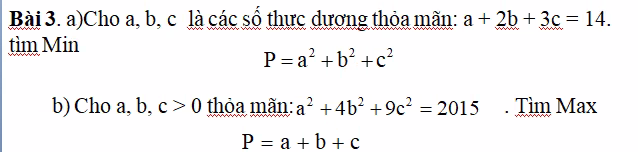a.
\(a+2b+3c=14\Rightarrow2a+4b+6c=28\)
\(P-28=a^2+b^2+c^2-2a-4b-6c\)
\(P-28=\left(a-1\right)^2+\left(b-2\right)^2+\left(c-3\right)^2-14\ge-14\)
\(\Rightarrow P\ge28-14=14\)
\(P_{min}=14\) khi \(\left(a;b;c\right)=\left(1;2;3\right)\)
b.
\(P^2=\left(a+b+c\right)^2=\left(1.a+\dfrac{1}{2}.2b+\dfrac{1}{3}.3c\right)^2\)
\(P^2\le\left(1+\dfrac{1}{4}+\dfrac{1}{9}\right)\left(a^2+4b^2+9c^2\right)=\dfrac{49}{36}.2015\)
\(\Rightarrow P\le\dfrac{7\sqrt{2015}}{6}\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(\dfrac{6\sqrt{2015}}{7};\dfrac{3\sqrt{2015}}{4};\dfrac{2\sqrt{2015}}{21}\right)\)