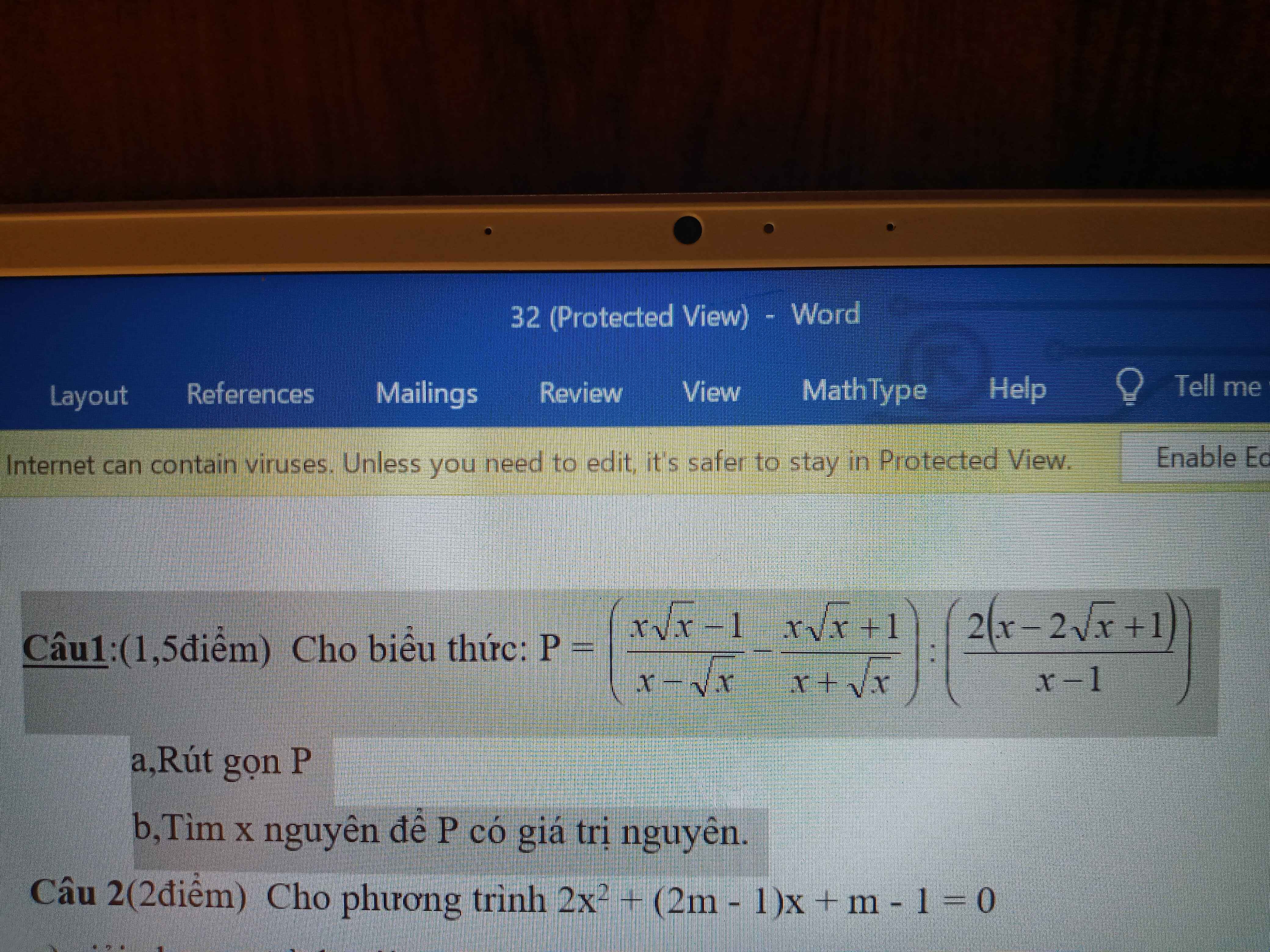
\(P=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(\dfrac{2\left(x-2\sqrt{x}+1\right)}{x-1}\right)\left(x>0,x\ne1\right)\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right):\dfrac{2\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}}:\dfrac{2\left(\sqrt{x}-1\right)}{\sqrt{x}+1}=2.\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để \(P\in Z\Rightarrow2⋮\sqrt{x}-1\Rightarrow\sqrt{x}-1\in\left\{1;2;-1;-2\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{2;3;0\right\}\Rightarrow x\in\left\{4;9;0\right\}\)
a) Với x>0; x≠1 ta có:
\(P=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right).\left(\dfrac{2\left(x-2\sqrt{x}+1\right)}{x-1}\right)\)
\(=\left(\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right).\left(\dfrac{2\left(\sqrt{x}-1\right)^2}{x-1}\right)\)
\(=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right).\left(\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{2\sqrt{x}}{\sqrt{x}}\right).\left(\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)}\right)=\dfrac{4x-4\sqrt{x}}{\sqrt{x}+1}\)
Vậy....
a) Ta có: \(P=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(\dfrac{2\left(x-2\sqrt{x}+1\right)}{x-1}\right)\)
\(=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}:\dfrac{2\left(\sqrt{x}-1\right)}{\sqrt{x}+1}\)
\(=2\cdot\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b) Để P nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow2⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{2;3\right\}\)
hay \(x\in\left\{4;9\right\}\)








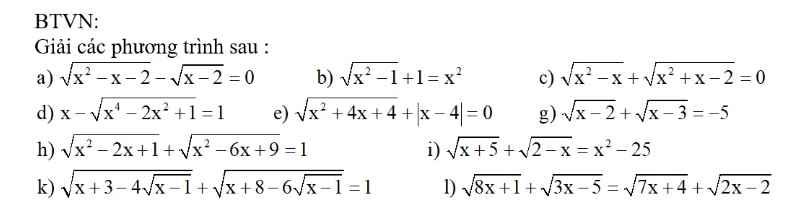

 Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ
Ai giúp em với ạ em cần rất gấp bài 4 thôi ạ