Bài 8:
\(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
\(=\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}\right)\)
Đặt \(B=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}\)
=>\(A=\dfrac{1}{4}B\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{50^2}< \dfrac{1}{49\cdot50}=\dfrac{1}{49}-\dfrac{1}{50}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\)
=>\(B=1+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}< 1+1-\dfrac{1}{50}=2-\dfrac{1}{50}\)
\(\Leftrightarrow A=\dfrac{1}{4}B< \dfrac{1}{4}\left(2-\dfrac{1}{50}\right)=\dfrac{1}{2}-\dfrac{1}{200}< \dfrac{1}{2}\)
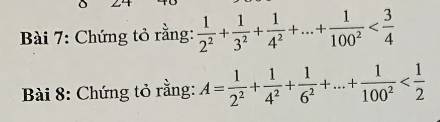 \
\ 
