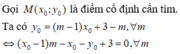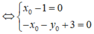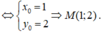Các câu hỏi tương tự
Đồ thị của hàm số x = (m-1)x + 3 - m (m là tham số) luôn đi qua một điểm M cố định có tọa độ là
A. M(0;3)
B. M(1;2)
C. M(-1;-2)
D. M(0;1)
Đồ thị của hàm số y
x
2
+2mx - m +1 (m là tham số) luôn đi qua một điểm M cố định có tọa độ là A. M(0;1) B. M
(
1
2
;
3
2
)
C. M
(
1
2
;
5
4
)
D. M(-1;0)
Đọc tiếp
Đồ thị của hàm số y = x 2 +2mx - m +1 (m là tham số) luôn đi qua một điểm M cố định có tọa độ là
A. M(0;1)
B. M ( 1 2 ; 3 2 )
C. M ( 1 2 ; 5 4 )
D. M(-1;0)
Biết đồ thị (Cm) của hàm số y (m+1)x + mx + m(m≢0) luôn đi qua một điểm M cố định khi m thay đổi. Tọa độ điểm M khi đó là A. B. C. D.
Đọc tiếp
Biết đồ thị (Cm) của hàm số y = (m+1)x + mx + m(m≢0) luôn đi qua một điểm M cố định khi m thay đổi. Tọa độ điểm M khi đó là
A. 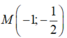
B. ![]()
C. ![]()
D. ![]()
Đồ thị của hàm số ![]() + mx + m ( m là tham số) luôn đi qua một điểm M cố định có tọa độ là
+ mx + m ( m là tham số) luôn đi qua một điểm M cố định có tọa độ là
A. M(-1;2)
B. M(-1;-4)
C. M(1;-2)
D. M(1;-4)
Biết đồ thị
(
C
m
)
của hàm số y = ![]() - 2m +3 luôn đi qua một điểm M cố định khi m thay đổi, khi đó tọa độ của điểm M là
- 2m +3 luôn đi qua một điểm M cố định khi m thay đổi, khi đó tọa độ của điểm M là
A. M(-1;1)
B. M(1;4)
C. M(0;2)
D. M(0;3)
Cho hàm số y = m + 1 x - 2 m + 1 x - 1 (m là tham số) có đồ thị (G).
Xác định m để đồ thị (G) đi qua điểm (0; -1).
Cho hàm số: y
x
3
− (m + 4)
x
2
− 4x + m (1)a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m 0d) Xác định k để (C) cắt đường thẳng y kx tại ba điểm phân biệt.
Đọc tiếp
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m = 0
d) Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số y
x
4
- m
x
2
- m -1 có đồ thị (C). Tọa độ các điểm cố định của
(
C
m
)
là A. B. C. D.
Đọc tiếp
Cho hàm số y = x 4 - m x 2 - m -1 có đồ thị (C). Tọa độ các điểm cố định của ( C m ) là
A. ![]()
B. ![]()
C. ![]()
D. ![]()