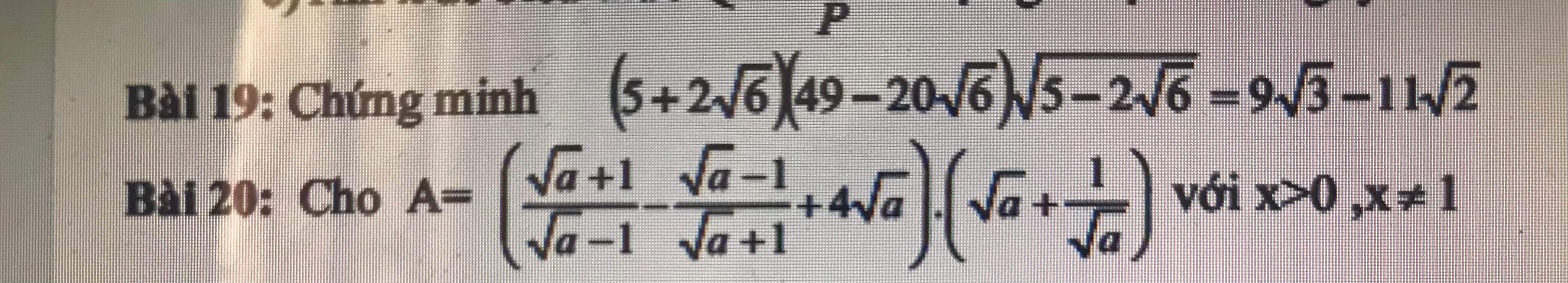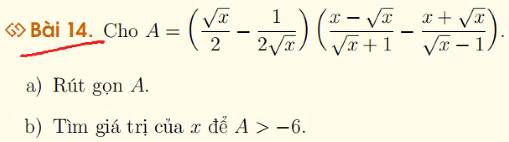\(A=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}+\dfrac{1}{\sqrt{a}}\right)\left(a>0,a\ne1\right)\)
\(A=\left[\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}-\dfrac{\left(\sqrt{a}-1\right)^2}{a-1}+4\sqrt{a}\right].\left(\dfrac{a+1}{\sqrt{a}}\right)\)
\(A=\left[\dfrac{\left(\sqrt{a}+1+\sqrt{a}-1\right)\left(\sqrt{a}+1-\sqrt{a}+1\right)}{a-1}+\dfrac{4\sqrt{a}\left(a-1\right)}{a-1}\right].\dfrac{a+1}{\sqrt{a}}\)
\(A=\left[\dfrac{4\sqrt{a}+4\sqrt{a}\left(a-1\right)}{a-1}\right].\dfrac{a+1}{\sqrt{a}}\)
\(A=\left[\dfrac{4\sqrt{a}\left(1+a-1\right)}{a-1}\right].\dfrac{a+1}{\sqrt{a}}\)
\(A=\dfrac{\left(4a\sqrt{a}\right)\left(a+1\right)}{\left(a-1\right)\sqrt{a}}=\dfrac{4a\left(a+1\right)}{a-1}=\dfrac{4a^2+4a}{a-1}\)