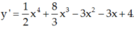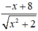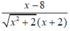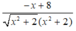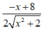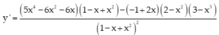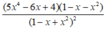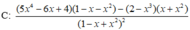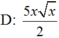\(y'=\dfrac{\left[\left(3x^2-5x\right)^5\right]'}{2\sqrt{\left(3x^2-5x\right)^5}}=\dfrac{5\left(3x^2-5x\right)^4.\left(3x^2-5x\right)'}{2\sqrt{\left(3x^2-5x\right)^5}}=\dfrac{5\left(3x^2-5x\right)^4.\left(6x-5\right)}{2\sqrt{\left(3x^2-5x\right)^5}}\)
\(=\dfrac{5\sqrt{\left(3x^2-5x\right)^3}.\left(6x-5\right)}{2}\)
Hoặc là:
\(y=\sqrt{\left(3x^2-5x\right)^5}=\) \((3x^2-5x)^{\frac{5}{2}}\Rightarrow y'=\dfrac{5}{2}.(3x^2-5x)^{\frac{3}{2}}.(3x^2-5x)'\)
\(=\dfrac{5\sqrt{\left(3x^2-5x\right)^3}.\left(6x-5\right)}{2}\)