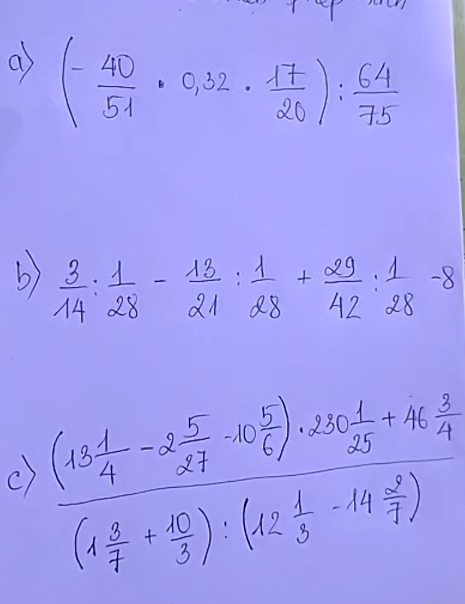Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=k.b\\c=k.d\end{matrix}\right.\)
a.
ta có:
\(\dfrac{3a+5b}{3a-5b}=\dfrac{3.kb+5b}{3.kb-5b}=\dfrac{b.\left(3k+5\right)}{b.\left(3k-5\right)}=\dfrac{3k+5}{3k-5}\) (1)
\(\dfrac{3c+5d}{3c-5d}=\dfrac{3.kd+5d}{3.kd-5d}=\dfrac{d\left(3k+5\right)}{d\left(3k-5\right)}=\dfrac{3k+5}{3k-5}\) (2)
(1);(2) \(\Rightarrow\dfrac{3a+5b}{3a-5b}=\dfrac{3c+5d}{3c-5d}\)
b.
Tương tự:
\(\left(\dfrac{a+b}{c+d}\right)^2=\left(\dfrac{kb+b}{kd+d}\right)^2=\left[\dfrac{b\left(k+1\right)}{d\left(k+1\right)}\right]^2=\left(\dfrac{b}{d}\right)^2=\dfrac{b^2}{d^2}\) (3)
\(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{\left(kb\right)^2+b^2}{\left(kd\right)^2+d^2}=\dfrac{k^2b^2+b^2}{k^2d^2+d^2}=\dfrac{b^2\left(k^2+1\right)}{d^2\left(k^2+1\right)}=\dfrac{b^2}{d^2}\) (4)
(3);(4) \(\Rightarrow\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
Các câu sau em có thể làm y hệt theo cách tương tự




 Cứu
Cứu