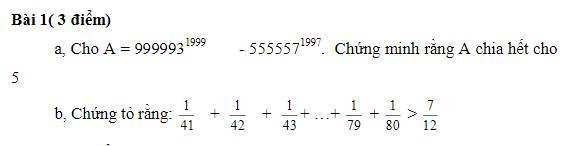a) Ta có:
\(A=999993^{1999}-555557^{1997}\)
\(A=\overline{...3}^{1999}-\overline{...7}^{1997}\)
\(A=\overline{...3}^{1996}\cdot\overline{...3}^3-\overline{...7}^{1996}\cdot7\)
\(A=\left(\overline{...3}^4\right)^{499}\cdot\overline{...7}-\left(\overline{...7}^4\right)^{499}\cdot\overline{...7}\)
\(A=\overline{...1}^{499}\cdot\overline{...7}-\overline{...1}^{499}\cdot\overline{...7}\)
\(A=\overline{...7}-\overline{...7}\)
\(A=\overline{...0}\)
Vậy A ⋮ 5 vì A có chữ số tận cùng là 0
b) Đặt: \(A=\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{79}+\dfrac{1}{80}\)
\(\Rightarrow A=\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{59}+\dfrac{1}{60}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+...+\dfrac{1}{79}+\dfrac{1}{80}\right)\)
\(\Rightarrow A>\left(\dfrac{1}{60}+\dfrac{1}{60}+...+\dfrac{1}{60}\right)+\left(\dfrac{1}{80}+\dfrac{1}{80}+...+\dfrac{1}{80}\right)\)
\(\Rightarrow A>\dfrac{20}{60}+\dfrac{20}{80}\)
\(\Rightarrow A>\dfrac{1}{3}+\dfrac{1}{4}\)
\(\Rightarrow A>\dfrac{7}{12}\)
Vậy: ...
a) để chứng mình A ⋮ ta xét số tận cùng của A bằng việc xét chữ số tận cùng của từng số hạng
ta có : \(3^{1999}\) = \(\left(3^4\right)^{499}.3^3=81^{499}.27\)
Suy ra: \(3^{1999}\) có tận cùng là 7
\(7^{1997}=\left(7^4\right)^{499}.7=2041^{499}.7\) ⇒7\(7^{1997}\) có tận cùng là 7
Vậy A có tận cùng bằng 0 ⇒ A ⋮ 5
b) Ta thấy: \(\dfrac{1}{41}\) đến \(\dfrac{1}{80}\) có 40 phân số.
Vậy \(\dfrac{1}{41}+\dfrac{1}{42}+\dfrac{1}{43}+...+\dfrac{1}{78}+\dfrac{1}{79}+\dfrac{1}{80}\)
\(=\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{59}+\dfrac{1}{60}\right)+\left(\dfrac{1}{61}+\dfrac{1}{62}+....+\dfrac{1}{79}+\dfrac{1}{80}\right)\)
Vì \(\dfrac{1}{41}>\dfrac{1}{42}.>...>\dfrac{1}{60}\) và \(\dfrac{1}{61}>\dfrac{1}{62}>...>\dfrac{1}{80}\)
Ta có \(\left(\dfrac{1}{60}+\dfrac{1}{60}+.....+\dfrac{1}{60}+\dfrac{1}{60}\right)+\left(\dfrac{1}{80}+\dfrac{1}{80}+....+\dfrac{1}{80}+\dfrac{1}{80}\right)\\ =\dfrac{20}{60}+\dfrac{20}{\dfrac{80}{ }}=\dfrac{7}{12}\)
Từ đó suy ra:
\(\dfrac{1}{41}+\dfrac{1}{42}+\dfrac{1}{43}+....+\dfrac{1}{78}+\dfrac{1}{79}+\dfrac{1}{80}>\dfrac{7}{12}\)