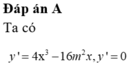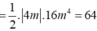Các câu hỏi tương tự
Tìm các giá trị của tham số m để đồ thị hàm số:
y
x
4
-
8
m
2
x
2
+
1
có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có diện tích bằng 64 A. Không tồn tại m B. ...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = x 4 - 8 m 2 x 2 + 1 có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có diện tích bằng 64
A. Không tồn tại m
B. m = 2 5
C. m = - 2 5
D. m = ± 2 5
Có bao nhiêu giá trị nguyên của tham số m để điểm M(2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số
y
2
x
3
-
3
(
2
m
+
1
)
x
2
+
6
m
(
m
+
1
)
x
+
1
(C) một tam giác có...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để điểm M(2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 (C) một tam giác có diện tích nhỏ nhất
A. 0
B. 1
C. 2
D. Không tồn tại
Có giá trị của tham số m để đồ thị hàm số y= x4-4( m-1) x2+2m-1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều. Hỏi số nguyên nào gần với số m nhất?
A. 2
B. 3
C. 4
D. đáp án khác
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
4
-
4
m
-
1
2
+
2
m
-
1
có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều. A. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 - 4 m - 1 2 + 2 m - 1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều.
A. 
B.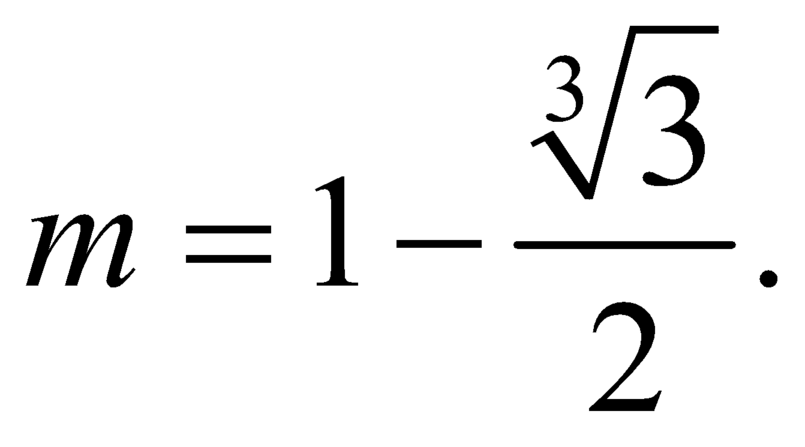 
C. 
D. 
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
4
-
4
(
m
-
1
)
x
2
+
2
m
-
1
có 3 điểm cực trị tạo...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 - 4 ( m - 1 ) x 2 + 2 m - 1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều
A. m = 0
B. m = 1
C. m = 1 + 3 3 2
D. m = 1 - 3 3 2
Cho hàm số: 
.Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có có bán kính đường tròn ngoại tiếp bằng 1.
A. 0
B. 1
C. 2
D. 3
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số
y
x
4
-
2
m
x
2
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. A. m 0 B. m 1 C.
0
m
4
3
D. 0 m 1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x 4 - 2 m x 2 có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
A. m> 0
B. m< 1
C. 0 < m < 4 3
D. 0< m< 1
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất cả các giá trị của tham số thực m để hàm...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = - 1 2
B. m = 1 2
C. m = 0
D. m = 1