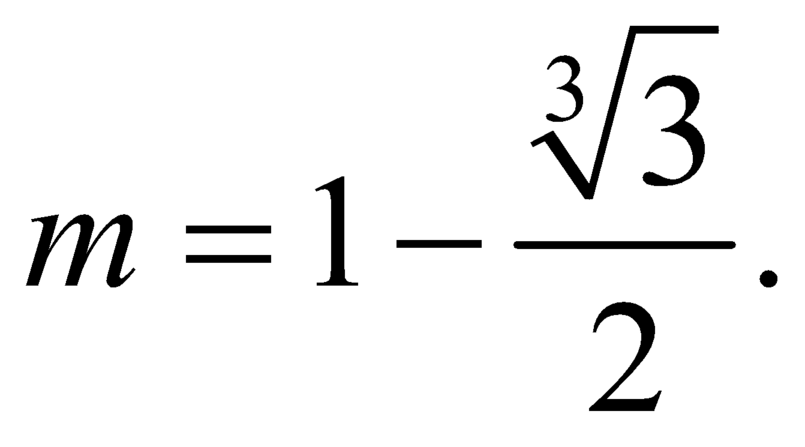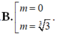Question

Có giá trị của tham số m  để đồ thị hàm số y= x⁴-4( m-1) x²+2m-1 có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều. Hỏi số nguyên nào gần với số m nhất?

A. 2

B. 3

C. 4

D. đáp án khác

Answer 1

Ta có  đao hàm y’ = 4x³- 8( m-1) x= 4x( x²- 2( m-1) )

 

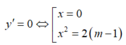
nên hàm số có 3 điểm cực trị khi m> 1.

Với điều kiện m > 1  đồ thị hàm số có 3 điểm cực trị là:

A ( 0 ; 2 m - 1 ) ,   B ( 2 ( m - 1 ) ; - 4 m 2 + 10 m - 5 ) , C ( - 2 ( m - 1 ) ; - 4 m 2 + 10 m - 5 ) .

Ta có: AB²= AC²= 2( m-1) + 16( m-1) ⁴; BC²= 8( m-1)

Để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều thì:

AB= AC= BC tương đương  AB²= AC²= BC²

Do đó: 2( m-1) + 16( m-1) ⁴= 8( m-1)

⇔ 8 ( m - 1 ) 4 - 3 ( m - 1 ) = 0  

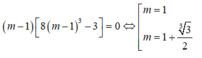
So sánh với điều kiện ta có: m = 1 + 3 3 2   thỏa mãn.

Chọn A.