Bài 1:
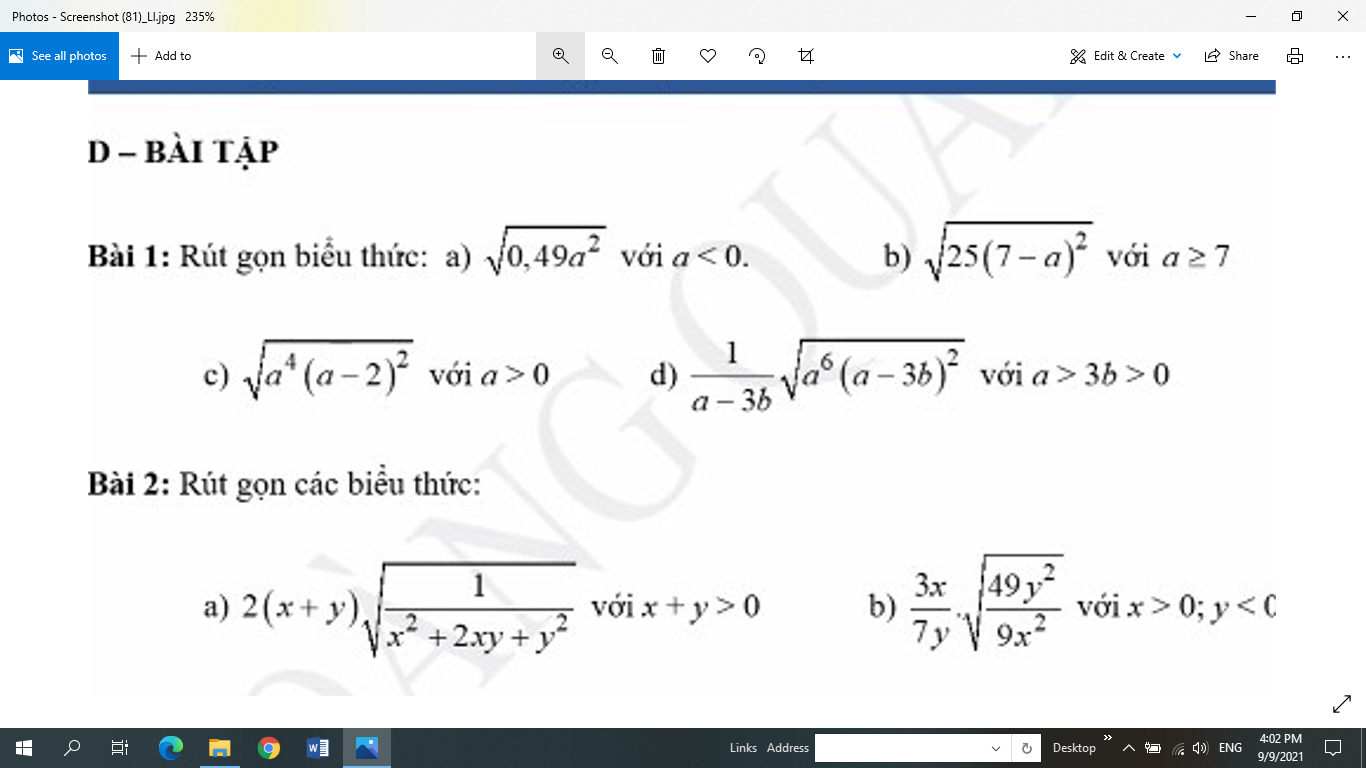
a: \(\sqrt{0.49a^2}=-0.7a\)
b: \(\sqrt{25\left(a-7\right)^2}=5a-35\)
c: \(\sqrt{a^4\left(a-2\right)^2}=a^2\cdot\left(a-2\right)\)
d: \(\dfrac{1}{a-3b}\cdot\sqrt{a^6\left(a-3b\right)^2}\)
\(=\dfrac{1}{a-3b}\cdot a^3\cdot\left(a-3b\right)=a^3\)
Bài 2:
a: \(2\left(x+y\right)\cdot\sqrt{\dfrac{1}{x^2+2xy+y^2}}\)
\(=2\left(x+y\right)\cdot\dfrac{1}{x+y}\)
=2
b: \(\dfrac{3x}{7y}\cdot\sqrt{\dfrac{49y^2}{9x^2}}\)
\(=\dfrac{3x}{7y}\cdot\dfrac{-7y}{3x}\)
=-1
\(1,\\ a,\sqrt{0,49a^2}\left(a< 0\right)=-0,7a\\ b,\sqrt{25\left(7-a\right)^2}\left(a\ge7\Leftrightarrow7-a\le0\right)=5\left(a-7\right)\\ c,\sqrt{a^4\left(a-2\right)^2}\left(a>0\right)=\left[{}\begin{matrix}a^2\left(a-2\right),\forall a\ge2\\a^2\left(2-a\right),\forall0< a< 2\end{matrix}\right.\\ d,\dfrac{1}{a-3b}\sqrt{a^6\left(a-3b\right)^2}\left(a>3b>0\right)=\dfrac{1}{a-3b}\cdot a^3\left(a-3b\right)=a^3\)