Question

Chứng minh rằng trung điểm các cạnh của một hình thoi là đỉnh của một hình chữ nhật.

Answer 1

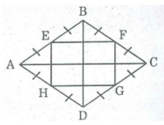
Giả sử hình thoi ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

* Trong ∆ ABC, ta có:

E là trung điểm của AB

F là trung điểm của BC

Nên EF là đường trung bình của  ∆ ABC.

⇒ EF // AC và EF = 1/2 AC (t/chất đường trung bình của tam giác) (1)

* Trong  ∆ ADC, ta có: H là trung điểm của AD

G là trung điểm của CD

Nên HG là đường trung bình của tam giác ADC

⇒ HG // AC và HG = 1/2 AC (t/chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Mặt khác: AC ⊥ BD (tính chất hình thoi)

EF // AC (chứng minh trên)