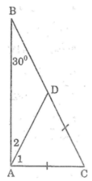
Xét ΔABC, ta có: ∠A= 90o; ∠B= 30o
Trên cạnh BC lấy điểm D sao cho CD = AC
Ta có: ΔACD cân tại C
Mà ∠C + ∠B = 90o (tính chất tam giác vuông)
Suy ra: ∠C = 90o - ∠B = 90o - 30o = 60o
Suy ra: ΔACD đều
Suy ra: AC = AD = DC và ∠A1= 60o
Ta có: ∠A1+ ∠A2 = ∠BAC = 90o
⇒ ∠A2 = 90o - ∠A1 = 90o - 60o = 30o
Trong ΔADB, ta có: ∠A2 = ∠B= 30o
Suy ra: ΔADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)
Hay AD = DB
Suy ra: AC = CD = DB mà CD + DB = BC
Vậy AC = 1/2 BC.